Definizio fisikoa eman aurretik azter ditzagun zenbait adibide:

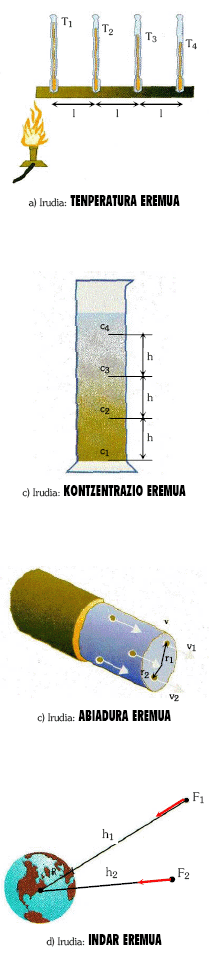1. ADIBIDEA: (a irudia) Barra metaliko bat bere mutur batetik berotzen badugu berehala ohartuko gara barran zehar tenperatura balio ezberdinak izango direla, tenperatura hauek barraren zein puntu eta berotzen pasa dugun denboraren menpekoak izanik. Kasu honetan TENPERATURA EREMU bat izango dugu.

2. ADIBIDEA: (b irudia) Buztinezko ur disoluzio batean KONTZENTRAZIO EREMU bat sortzen da. Denbora pasatzen doan heinean, buztinaren hauspeatzearen ondorioz, disoluzioa prestatu dugun ontzian disoluzio kontzentrazio ezberdinak izango ditugu neurketa egiten dugun altueraren arabera.

3. ADIBIDEA: Itsasoan murgiltzen den urpekari batek, itsas hondorantz urperatzerakoan, bere gainean nabaritzen duen presio hidrostatikoa geroz eta handiagoa izango da. Hemen ere ikusten da presioaren balioa aldatzen dela urpekariak ur barnean duen posizioaren arabera. Esan dezakegu PRESIO EREMU baten aurrean gaudela.

4. ADIBIDEA: (c irudia) Tutu batetik pasatzen den likido baten geruza ezberdinek, tutuaren paretekin likidoak duen marruskadura eta likido berak duen biskositatearen ondorioz, ez dute abiadura berdina: abiadura handiagoa eramango dute tutuaren erditik mugitzen diren likido geruzek tutuaren paretekin kontaktuan daudenak baino. Kasu honetan ABIADURA EREMU bat izango dugu.

5. ADIBIDEA: (d irudia) Lurraren inguruan kokatzen diren gorputzek Lurrarekiko erakarpen indar bat nabaritzen dute, erakarpen indar horren balioa Lurrarekiko gorputzaren distantziarekiko alderantziz proportzionala izanik. Kasu honetan INDAR EREMU bat izango dugu.

Adibide guzti hauetan oinarriturik, eman dezakegu eremuaren definizio fisikoa:

Espazioko eskualde konkretu bateko puntu bakoitzean eta denbora une konkretu bakoitzeko magnitude fisiko batek balio ezberdinak hartzen baditu, bertan EREMU bat existitzen dela esaten da.

EREMUEN PROPIETATEAK

Adibide hauen bitartez (adibide gehiago ere aipa genitzake: presio atmosferikoa, erliebearen altuera,…) ikusi dugu, neurtu nahi dugun magnitude fisikoaren arabera, espazioko eskualde ezberdinetan edozein motatako eremua defini dezakegula. Baina denetan deskribatu ditzakegu zenbait propietate garrantzitsu:

• Eremua definitzen duen magnitudeak (X) har ditzakeen balioak, kontsideratutako espazioko puntuaren eta denbora unearen funtzioak dira.

X=X(x,y,z,t)

Honen arabera ikusi dezakegu 1., 2., eta 3. adibideak EREMU LINEALAK direla magnitudearen balioak norabide bakar batean aldatzen baitira; 4. adibidea EREMU LAUA da (bi dimentsiotan hedatzen baita); eta 5. adibidea EREMU ESPAZIALA da.

• Eremu batzuetan neurtzen den magnitudearen balioa ez da denborarekin aldatzen: eremu hauei EREMU EGONKORRAK (“estacionario”) deritze. Honen adibidea Lurrak bere inguruan sortzen duen eremu grabitatorioarena da.

• Eremua definitzen duen magnitudearen arabera, EREMUA ESKALARRA (1., 2., eta 3. adibideak) edo EREMU BEKTORIALA (4. eta 5. adibideak) izan daiteke.

Eremua erabat zehaztuta egon dadin, beharrezkoa da bertan ageri den magnitudearen balioa, norabidea eta norantza, bektorea bada, edo soilik balioa eskalarra bada, zeharo definituta egotea.

• Eremua definitzen duen magnitudearen balioa espazioko puntu guztietan berdina bada (X=X(x,y,z,t)=kte) EREMUA UNIFORMEA dela esaten da; hala ere kasu gehienetan magnitudearen balioa posizioaren arabera aldatu egiten da. Azken hauen artean badaude zenbait eremu puntu finko batetik hasita magnitudearen balioa era erradial batean aldatzen direnak. Eremu hauei EREMU ZENTRALAK deitzen zaie (5. adibidea).