Orain arte ikusi dugunaren arabera, eremu grabitatorioan aurkitzen den m masako gorputz baten gainean indar bat agertzen da, berau, gorputzak duen posizioaren araberakoa izanik.

Honen arabera, partikularen posizioa aldatzerakoan, eremuko indar horrek lan bat egingo du adierazpenak emango diguna.

Bestalde, indar grabitatorioa indar zentrala da, bere norabidea beti eremua sortzen duen masaren zentrora zuzenduta dago. Erraz froga daiteke, indar zentral guztiak kontserbakorrak direla (ikus alboko koadroa), beraz, indar grabitatorioa ere kontserbakorra da eta esaten da EREMU GRABITATORIOA KONTSERBAKORRA dela.

Eremu grabitatorioaren barnean m masa bat posizioz aldatzen bada (A puntu batetik B beste puntu batera) bere gainean eragiten duen indar grabitatorioak (kontserbakorra) egiten duen lana ez da ibilbidearen menpekoa, baizik eta, hasierako eta bukaerako posizioen baitan bakarrik dagoen magnitude eskalar baten menpe. Azter dezagun egoera hau era sakonago batean:

Suposa dezagun M masa finko batek sortzen duen eremu grabitatorioaren barnean m masako partikula bat A puntu batetik B puntu batera desplazatu nahi dela. Indar grabitatorioak egiten duen lana zera izango da:

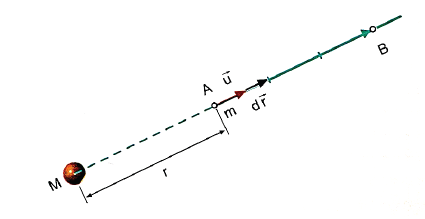
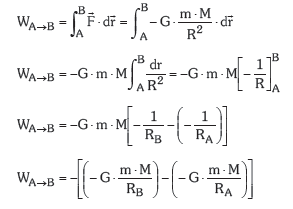
Indar grabitatorioak A eta B puntuen artean m masa bat posizioz aldatzerakoan egiten duen lana, A eta B puntuetan magnitude eskalar berri batek hartzen dituen balioen anteko diferentziaren berdina izango da.

Magnitude eskalar berri honi ENERGIA POTENTZIALA (Ep) deritzo:

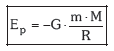
Ondorioz, eremuko indarrak egiten duen lana honela adierazi daiteke:

Azken adierazpen honek lanaren balioa bi puntuen artean dagoen energia potentzialaren diferentziarekin erlazionatzeko balio digu baina ez digu puntu konkretu batean energia potentzialaren balioa zehazteko balio. A puntu batean m masako gorputz batek duen energia potentziala zehaztu nahi badugu, nahikoa da infinituan kokatuta dagoen B puntu hartzea eta elkarren arteko energia potentzialen diferentzia eremuko indarrak egiten duen lanarekin berdintzea:

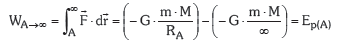
Honen arabera, energia potentzialaren definizio fisikoa hau izango dugu:

P puntu batean aurkitzen den m masa baten energia potentzial grabitatorioa, m masa hori puntu honetatik infinituraino eramateko €eremu grabitatorioak egiten duen lana da.

POTENTZIAL GRABITATORIOA

Indar grabitatorioarekin gertatzen zen bezala, energia potentzialaren balioa puntu batean, bertan dagoen m masaren balioaren araberakoa izango da. m masa honek duen energia potentziala eta masa beraren arteko zatidurak, masa unitatearen energia potentziala emango digu eta magnitude hau eremuko puntu bakoitzean konstantea izango da. Erlazio honi POTENTZIAL GRABITATORIOA deritzo.

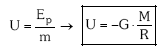
Honela defini daiteke:

Masa unitatea P puntu batetik infinituraino eramateko indar grabitatorioak egin behar duen lana da.

Masa unitatearen ordez, m masa bat A-tik B-ra desplazatu nahi bada, eremu grabitatorioak egingo duen lana zera izango da:

GAINEZARMEN PRINTZIPIOA

Espazioko eskualde batean masa puntual bat baino gehiago baldin badago, guztien artean P puntu batean sortutako potentzial grabitatorioaren balioa kalkulatzeko, gainezarmen printzipioa aplikatuz, masa bakoitzari dagokion potentzialaren arteko batura kalkulatu beharko da:

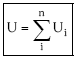
GAINAZAL EKIPOTENTZIALAK

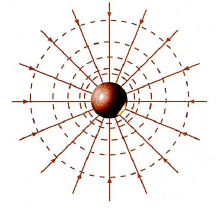Potentzial grabitatorioaren balioa berdina den eremuko puntuak elkartzerakoan, gainazal ezberdinak lortzen ditugu GAINAZAL EKIPOTENTZIALAK deitzen direnak.

• Gainazal hauek eremu lerroekiko elkarzutak dira edozein puntuan.
• Eremu grabitatorioak egiten duen lana masa bat gainazal ekipotentzialaren bi puntuen artean desplazatzeko nulua da:

• Masa puntual batentzat, honekiko distantziakideak diren puntu guztiek potentzial grabitatorio berdina dutenez, masan zentroa duten esfera zentrukideak dira.

Kontutan hartzekoak

A) Eremu bat kontserbakorra dela esaten da, partikula bat bi punturen artean desplazatu nahi denean, egin behar den lana jarraitutako ibilbidearekiko askea denean.

Azter dezagun adibide bat: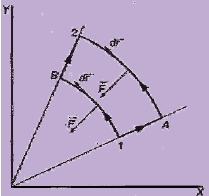

Partikula bat 1etik 2ra eraman nahi badugu, bi bide aukeratu ditzakegu: 1B2 edota 1A2.

1B2 bidea:

Partikula 1etik Bra desplazatzeko egin behar den lana nulua da:  da,  delako.

Beraz egin beharreko lana  izango da.

1A2 bidea:

1etik Ara egin beharreko lana -ren berdina izango,  bait da ere.

 = direnez, garbi dago bi bideetatik egindako lana berdina dela.

Ondorioz, frogatuta geratzen da indar eremu zentralak kontserbakorrak direla.