Demagun orain eroale zuzen eta mugagabea dugula eta bertatik I intentsitateko korronteak zirkulatzen duela. Korronte lerrozuzen honek, eroaletik urrunduta dagoen P puntuan sortzen duen indukzioa zein den kalkulatuko dugu.
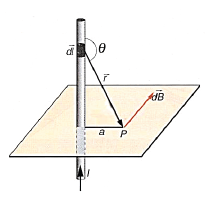Horretarako, har dezagun I korronte intentsitateak igarotzen duen eroale baten 
luzerako zati elementala (bere norabidea eta norantza korronte elektrikoarena delarik). Elementu honetan dagoen karga infinitesimala (dq) v abiadurarekin higitzen bada eroalean zehar, dl luzera burutzeko behar duen denbora ondokoa da:
Bestalde:
Beraz:
Horrela karga elementalak P puntuan sortzen duen eremu magnetiko elementala kalkulatu ahal izango dugu, aurreko atalean lortutako adierazpen matematikoan oinarriturik:
. dq kargarentzat: 
Azken adierazpen hau era bektorialean adierazita:
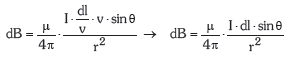
Azken adierazpen hau Laplacen Bigarren Legea izenez ezagutzen da.
Korronte lerrozuzena elkarren segidako infinitu dl korronte-elementuz osatuta dagoela suposa daiteke, hauetariko bakoitzak P puntuan 
eremua sortzen duelarik. P puntuan korronte lerro osoak sortuko duen indukzio magnetikoa kalkulatzeko, eremu elemental guztien batura kalkulatu beharko dugu. Horretarako aurreko adierazpena integratu beharko dugu:
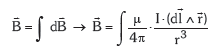
Eragiketak eginez ondorengo adierazpenera heltzen gara:
Lege honi BIOT-SAVARTEN LEGEA deitzen zaio.
Eroale lerrozuzen mugagabeak puntu jakin batean sortzen duen eremu magnetikoaren balioa, korrontearen intentsitatearekiko zuzenki proportzionala da eta alderantziz proportzionala eroalearen eta kontsideratutako puntuaren artean dagoen distantziarekiko.
Lortu dugun adierazpenak P puntuan agertzen den eremu magnetikoaren modulua adierazten du. Norabidea eta norantza zehazteko korronte elektrikoak sortzen duen eremu magnetikoaren indar lerroak zehaztea besterik ez dugu. Horretarako nahikoa da hari eroale zuzen batek zeharkatzen duen kartulina zati batean burdin txirbilak ipintzea. Hauek kartulinaren gainean korronte lerroan zentroa duten zirkunferentzi zentrukideak adierazten dituzte, eroalearekiko plano perpendikularrean daudelarik irudian agertzen den bezala.
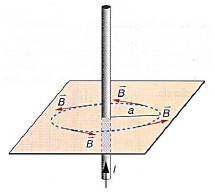Honen arabera, hari eroale zuzen eta mugagabe batek sortzen duen eremu magnetikoaren ezaugarriak hauek dira:
- MODULUA:
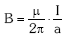adierazpenak ematen digu. - NORABIDEA: hari eroalearekiko perpendikularra da.
- NORANTZA: sakakortxoaren erregelaren araberakoa.
Ariketa Ebaztuak
4.- A(0,0) eta B(0,3) puntuetan dauden bi eroale lerrozuzen paralelo eta mugagabeetatik bi korronte igarotzen dira: IA=5 A eta IB=4 A, biak XY planoarekiko elkarzutak izanik, lehenengoa gorantz eta bigarrena beherantz eroaten dutelarik korronte elektrikoa. Kalkulatu eremu magnetikoa P(4,3) puntuan. (Ebazpena – pdf, 35kb)
Ariketa Proposatuak
5.- 
erreferentzi sisteman OY ardatzaren norabidean kokatutako hari eroale batek, 10 A-tako intentsitatea du ardatzaren norantza positiboan. Honetaz gain 
T-ko eremu magnetiko bat ere baldin badago, aurkitu ezazu A(0,0,1), B(1,0,0) eta C(0,0,-1) puntuetan (S.I.-ko unitateetan) agertzen den eremu magnetiko ordezkariaren modulu, norabide eta norantza.
6.- Bi hari eroale lerrozuzen eta mugagabetik 5 A-tako korronteak eroaten dira. Bi hari hauek elkar gurutzatu egiten dira norabide perpendikularretan eta 3 m-tako distantzia batera. Bata I-H norabidean ipintzen bada (korrontea iparrerantz eroaten delarik) eta bestea M-E norabidean (korrontea ekialderantz eroaten delarik), aurkitu ezazu eremuaren intentsitate bektorea bi hariak elkar gurutzatzen diren posizioa eta bi hariekiko distantziakidea den puntu batean. Hariak lurgainazaletik 7 eta 10 m-ra badaude, hurrenez hurren, zenbat balio du eremuaren intentsitate bektoreak lurgainazalean?.