Aurreko kasuan bezala, korronte zirkular bakoitza bere eremua sortzen duen korronte lerrozuzeneko elementuez eratuta dagoela suposa dezakegu.

Irudiko espirako (R erradioduna) O zentroan dagoen indukzio magnetikoa kalkulatuko dugu; espiratik I intentsitateko korronteak zirkulatzen duela izan behar dugu kontutan. Horretarako, espira korronte elementu infinituek osatzen dutela joko dugu.

Laplacen bigarren legea aplikatuz:

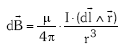
Espiraren zentroan agertzen den eremu magnetikoaren balioa aurkitzeko, korronte elementu guztiek sortzen duten eremu infinitesimalen batura egin beharko dugu, hau da, goiko adierazpenaren integrala kalkulatu beharko dugu:

Espira baten kasurako integralaren emaitza ondorengoa da:

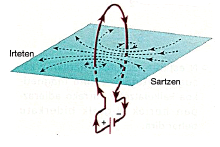
Lehen esan bezala, indukzio magnetikoaren norabidea eta norantza zehaztea beharrezkoa da. Honela, espira batek zeharkatutako kartulina batean burdin txirbilak jarriko bagenitu argazkian agertzen den bezalako lerroak ikusiko genituzke. Eremu lerro hauek espiraren planoarekiko perpendikularrak espirako planoaren puntuentzat eta beraien norantza eroaletik pasatzen den korronte elektrikoaren menpekoa izango da.

Laburbilduz, espira batek bere barruan sortzen duen eremu magnetikoaren ezaugarriak hauek dira:

• MODULUA: aurrean ikusitako adierazpenak ematen digu:
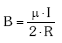
• NORABIDEA: espiraren planoarekiko elkarzuta.
• NORANTZA: sakakortxoaren erregelaren araberakoa.

Ariketa Proposatuak

7.- Beheko irudian zenbait espira dituzue: espirotatik doan korronte elektrikoak (espiraren planoarekiko perpendikularra) sortutako eremu magnetikoak espira horiek zeharkatzen ditu. Adierazi kasu bakoitzean korronteak daukan norantza.

8.- r₁ eta r₂ erradioak dituzten bi espira zentrukideetatik I1 eta I2 intentsitateko korronteak zirkulatzen dute.

1. Nola kokatu behar dira espirak eremu magnetikoaren intentsitate totala espiren zentroan nulua izatea nahi bada?
2. Kasu honetan nolakoak izan beharko lirateke korronteen norantzak?.
3. Zein izan beharko da bien arteko erlazioa?