Iazko ikasturtean oinarrizko higidura multzo baten azterketa egin ondoren (higidura zuzenak eta zirkularrak, uniformeak eta azeleratuak), aurten naturan hain arruntak diren higidura oszilakorren azterketa egingo dugu. Oszilazio guztien artean azterketa errazena Higidura Harmoniko Sinplearena (HHS aurrerantzean) da. Fisikak naturako fenomenoen behaketaz gain hauen formulazio matematikotaz ere arduratzen denez hori izango da jarraian agertzen ahaleginduko garena.

Higidura hau nolakoa den aztertzeko Higidura Zirkular eta Uniformearekin (HZirkU) alderatuko dugu. Azken finean, osziladore harmoniko baten joan etorria puntu baten inguruan HZirkU-z biraka dabilen partikula baten posizioaren proiekzioa diametroetako batekiko da.

Applet honen azterketa sakona egiten badugu ondorengoak ondoriozta daitezke:

• Osziladorearen posizioaren aldaketa biraka dabilen gorputzaren abiadurarekin harreman estua gordetzen du: are eta abiadura zirkular handiagoa posizio aldaketa azkarragoa eta, ondorioz, periodo txikiagoa, eta alderantziz.
• Nahiz eta biraka dabilen gorputzak abiadura konstantea eraman, osziladorearen abiadura ez da berdina oszilazio oso batean: azkarrago desplazatzen da oszilazio zentrotik pasatzerakoan eta geldiago doa muturretan.
• Abiaduraren aldaketa EZ DA UNIFORMEA: denbora tarte jakin batean abiaduran ematen den aldaketa (azelerazioa, hain zuzen ere) ez da konstantea, azelerazio desberdinak adierazten ditu oszilazioko posizio bakoitzean.

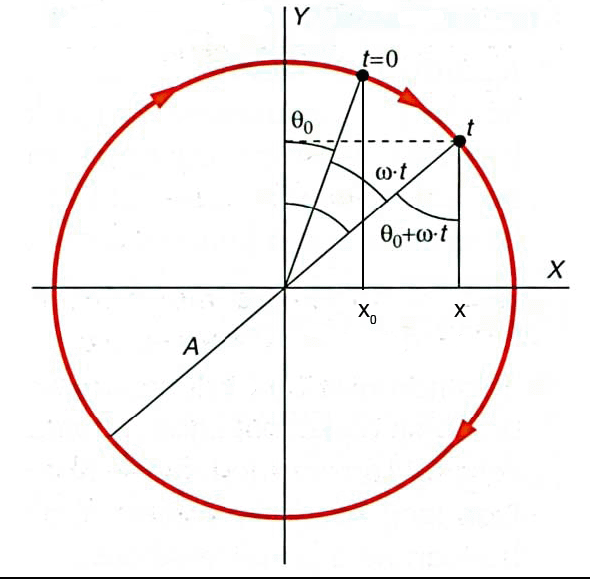Behaketa soilaren ondorioz jasotako informazio hori kontutan izanik, saia gaitezen aurrekoari erantzungo dion higiduraren ekuazioa lortzen. Horretarako aintzat hartuko dugu ezkerreko irudia:

• Jo dezagun t=0 denbora unean biraka dabilen gorputzaren posizio bektoreak OY ardatzarekiko osatzen duen angelua θ₀ dela.
• Kontutan izanik higikariak daraman ω abiadura angeluar konstantearekin t denbora tarte batean deskribatzen duen angelua ω·t dela, denbora tarte horren ondoren higikariaren posizio bektoreak OY ardatzarekiko osatuko duen angelua θ=ω·t+θ₀ izango da. 

Aurrean esan dugun bezala, gure helburua zera da: mugimendu zirkularrarekin higitzen den higikari horren posizioaren OX ardatzarekiko proiekzioaren azalpena egitea, proiekzio edo itzalaren mugimendua delako, hain zuzen ere, HHS. Azter dezagun, beraz, nola aldatzen den proiekzioaren posizioa jatorri puntuarekiko OX ardatzean zehar.

• t=0 unean: 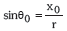 izango da. Zirkuluaren erradioa bat dator proiekzioaren desplazamendu maximoarekin, hau da, r=A. Beraz, 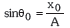eta, ondorioz, .
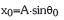• Egin dezagun orain azterketa bera t denbora unerako: 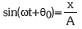eta, ondorioz,

HHS-aren berezko magnitudeak

1. OSZILAZIOA: joan etorriko higidura oso batean partikulak ibilitako espazioa.
2. OSZILAZIO ZENTROA edo JATORRIA (O): partikularen ibilbidearen bi muturren arteko distantziaren erdigunea.
3. ELONGAZIOA (x): osziladoreak jatorriarekiko daukan posizioa adierazten du. Metrotan adierazten da. Magnitude bektoriala denez, higikaria oszilazio zentroaren alde batean edo bestean egon, bere balioa positiboa edo negatiboa izango da.
4. ANPLITUDEA (A): gehienezko elongazioa da. Hau ere metrotan.
5. PERIODOA (T): partikulak oszilazio oso bat deskribatzeko behar duen denbora. Segundotan adierazten da.
6. MAIZTASUNA (f): denbora unitateko, hau da, segundo bakoitzeko partikulak egindako oszilazio kopurua. Matematikoki periodoaren alderantzizkoa da 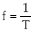. Bere unitatea s-1 edo Hertz da.
7. PULTSAZIOA (ω): partikulak duen abiadura angeluarra periodo batean oszilazio oso bat egiteko 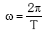. Abiadura angeluarra izanik azken finean bere unitateak rad/s dira.
8. FASEA (θ=ω·t+θ₀): osziladore harmonikoaren posizioa finkatzen duen angelua. Radianetan adierazten da.
9. HASIERAKO FASEA (θ₀): higidura hasten denean partikularen hasierako posizioa ematen digu. Hau ere, noski, radianetan. 

Kontutan hartzekoa

A) Aipatu beharra dago, partikularen mugimenduaren jatorri puntu bezala OSZILAZIO ZENTROA hartu dugula. Zenbait testu liburutan jatorria +A-n hartzen da. Kasu honetan, higikariak guk kontsideratu dugun jatorriarekiko p/2-ko desfasea darama. Ondorioz, higikariaren mugimenduaren ekuazioaioa horrela geratuko litzakete: x=A·sin(ωt-θ₀+π/2) edota x=A·cos(ωt+θ₀)

B) Osziladore harmonikoak bere mugimenduan daraman abiadura konstantea ez denez, bere desplazamendua EZ DA denborarekiko proportzionala

C) Fasea angelu bat izanik, Sistema Internazionalean RADIANETAN adierazten da.