Aurreko saioan ikusi ahal izan genuen osziladore harmonikoaren posizio nola aldatzen den denborarekiko (). Kontutan izanik posizioaren balioak funtzio sinusoidal baten bitartez emanak datozela garbi dago posizioaren balioak denborarekiko adieraziz gero ardatz kartesiarretan sinusoide bat lortuko dugula simulazio honetan ikusten den bezala (OHARRA: simulazioa ondo ikusi ahal izateko beharrezkoa da lehenik goiko menutik aukeratzea. Era egokian ikusi ahal izateko Internet Explorer beharrezkoa da).

Aurkitu ditzagun jarraian osziladorearen abiadura eta azelerazioak:

Osziladorearen abiadura

HHS baten abiadura kalkulatzeko abiaduraren definizio matematikoa izango dugu kontuan:

bektorea konstantea denez:

Beraz eta moduluan

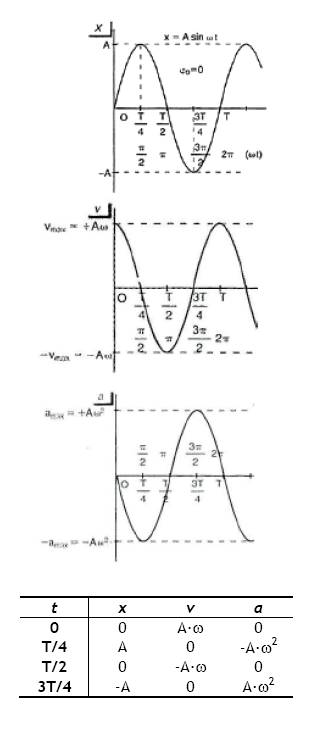
Ezkerreko irudian agertzen da osziladorearen abiaduraren aldaketa periodo batean nola ematen den.

Osziladorearen azelerazioa

Azelerazioak denbora unitateko abiaduraren aldaketa adierazten du. Hemen ere definizio matematikora jotzen badugu:

Moduluan

Abiaduraren kasuan bezala irudian azelerazioaren aldaketa denborarekiko nola ematen ikus ahal dezakezue. Bestalde, grafikoen azpian hiru magnitude zinematikoek periodo laurden bakoitzean hartzen dituzten balioak ikus ahal ditzakezue. Har ezazue tartetxo bat balio horien interpretazioa egiteko eta saia zaitezte aurretik egindako higiduraren analisiarekin erlazionatzen.

Arretaz behatzen baditugu posizioaren eta azelerazioaren ekuazioak antza handia dutela ikusiko dugu:

Hau da, Osziladore harmonikoaren azelerazioa bere posizioarekiko proportzionala da beti eta aurkako ikurra du.

Hhs-an azelerazioa eta elongazioa proportzionalak dira baina aurkako norantzakoak. Propietate hau da HIGIDURA HARMONIKO SINPLEAREN DEFINIZIO ZINEMATIKOA, hain zuzen ere.

Ebaztutako Ariketa

3.- HHS batean anplitudea 10 cm-koa da eta maiztasuna 100 ziklo/s-koa. Aurkitu itzazu osziladorearen elongazioa, abiadura eta azelerazioa t=0,0089 s denean. (Ebazpena, pdf-29,32 KB)

4.- Partikula batek higidura harmoniko sinplea dauka; anplitudea 0,1 m-koa da eta maiztasuna 40 Hz-takoa. Kalkulatu partikula horrek izango duen abiadura x=0,05 m posiziotik igarotzen denean. (Ebazpena, pdf-37,84 KB)

Proposatutako Ariketak

Ariketekin hasi baino lehen ohar pare bat. Lehenik eta behin, ariketan planteatzen den egoera zein den identifikatzea gomendatzen dizut. Ondoren ariketa behar den moduan planteatu, justifikatu eta azkenik, noski, matematikoki ebaztu, emaitza zuzena lortuz. Beraz, ez dira onartuko garapen eta ebazpide matematiko hutsak, Fisikaren puntutik eman daitezkeen azalpen edo justifikaziorik gabe. Ahalegin berezia ipini behar duzu ondorengo ataletan:

• Ariketa eta galderen garapenaren planteamendu eta justifikazio zuzentasunean
• Fisikaren legeen identifikazio eta erabilera zuzenetan
• Pausoz pausoka eginiko garapen, marrazki eta eskemen erabilpenean
• Oinarrizko kontzeptuen azalpena eta beraien aplikazio zuzenean
• Unitateen erabilera zuzenean

5.-Irakur itzazu ondorengo baieztapenak eta arrazoitu ezazu egia ala gezurra diren:

1. v(t) grafikoa π/2 rad desplazaturik aurkitzen da x(t)-renarekiko
2. a=0 eta v=0 badira, partikula oszilazio zentroan aurkitzen da.

6.-Aurkitu itzazu HHS baten periodoa eta elongazioaren ekuazioa baldin eta azelerazioaren adierazpena a=-2x bada eta anplitudeak 0,01 m balio badu.
7.-Partikula batek 10 cm aldendurik dauden bi punturen artean oszilatzen du, 2 s-ko periodoa duen mugimendu sinusoidal batekin.

1. Idatz ezazu partikularen mugimenduaren ekuazioa
2. Adierazi ezazu bere abiadura denboraren baitan
3. Zein balioen artean dago partikularen abiadura?
4. Aurkitu ezazu partikularen azelerazio maximoa.

8.-Partikula bat 5 cm-ko anplitude eta 40 m/s-ko abiadura maximoko higidura harmoniko sinplea deskribatzen du. Kalkulatu:

1. Partikularen bibrazio maiztasuna.
2. Azelerazio maximoa
3. Partikularen abiadura oreka posiziotik 2 cm-ra dagoenean.