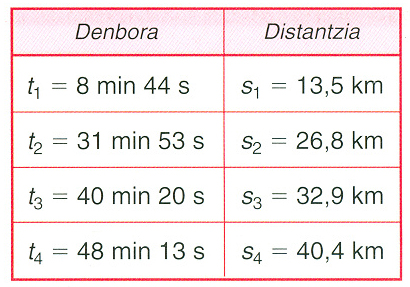
Alboko taulan Oscar Pereiro ziklista galiziarrak 2006ko Tourrean erlojuaren aurkako proban eginiko tartekako markak adierazten dira. Datu horiek ikusita, galdera hauek egin ditzakegu: oso bizkorra izan al da Oscar Pereiro? Denbora guztian bizkortasun berberaz higitu al zen? Galdera hauei erantzuteko, abiadura kontzeptua sakonki aztertu beharko dugu.

Batezbesteko abiadura

Batez besteko abiadura, , desplazamendu bektoreak adierazten duen posizio aldaketaren eta aldaketa gertatu arte igarotzen den denboraren arteko erlazioa da.

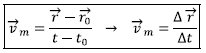
Definizioaren arabera (bektore eta eskalare baten arteko zatidura) batez besteko abiadura magnitude bektoriala dela ziurta dezakegu:

• MODULUA: desplazamendu bektorearen moduluaren eta pastutako denbora tartearen arteko zatidurarekin bat dator. SI sistemako abiadura-unitatea metro segunduko (m/s) da.
• NORABIDEA: desplazamenduaren (bektorea) eta denbora tartearen (eskalarea) arteko zatidura denez, bektoreen propietateetan oinarriturik, batez besteko abiaduraren norabidea desplazamendu bektorearen berdina da.
• NORANZKOA: aurrean adierazitakoaren arabera, desplazamendu bektorearen noranzkoarekin bat dator ere.

Aldiuneko Abiadura

Batez besteko abiadurak higikariak denbora-tarte konkretu batean duen portaerari buruzko informazioa ematen digu. Baina bere balioan oinarrituz, ezindugu jakin zein den higitzen ari den gorputzaren abiadura une bakoitzean. Adibidez, higikariak A puntutik aurrera azelera dezake eta jarraian bere abiadura poliki-poliki txikitu B puntura heldu arte; edota A-tik geldi-geldi abiatuz, B punturaino heldu arte bortizki azelera dezake. Aukera ugari egon daitezke, eta denetzat batez besteko abiadura berbera izan.

Beraz, batez besteko abiadura bera duten higidura mota desberdinak ezberdindu nahi baditugu, beharrezkoa dugu higikariak aldiune konkretu bakoitzean duen portaera aztertzea.

Begiratu beheko irudian zer gertatzen den batez besteko abiaduraren adierazpenean gero eta denbora tarte txikiagoak hartzen ditugunean, hau da, ∆t-k zerorantz jotzen duenean .

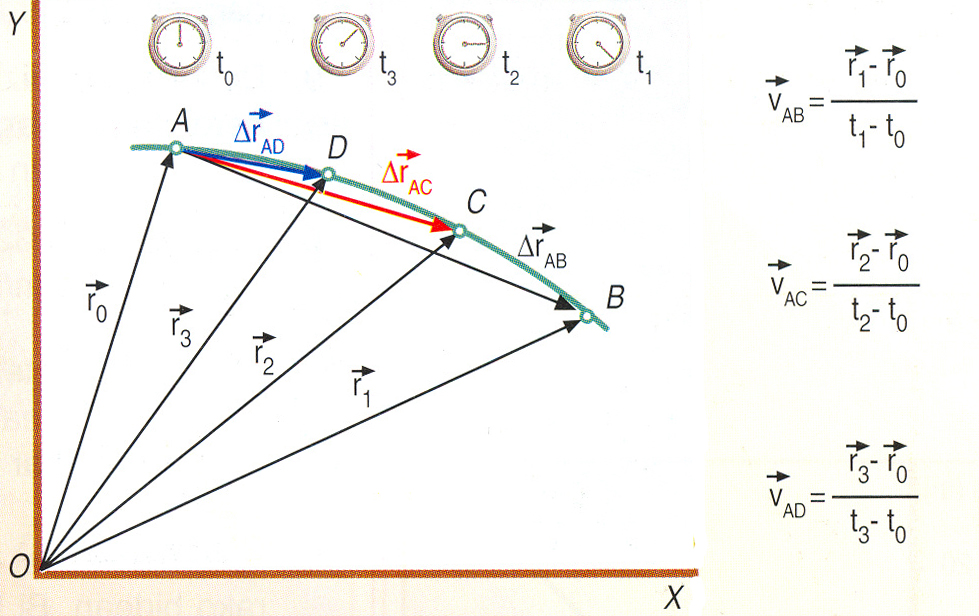
• Desplazamendu bektorea, 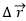, ibilbidearekiko ebakitzailea denez, ibilbidera hurbiltzen doa eta azkenerako ibilbidearekiko ukitzailea da.
• Desplazamendu bektorearen modulua, , egindako distantziara, 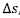, hurbiltzen da.
• Batez besteko abiadura bektorea abiadura bektorera hurbiltzen da t₀ unean. Bektore horri aldiuneko abiadura esaten zaio eta adierazteko 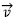 erabiltzen da.

Beraz, batez besteko abiadura bektoreak aldiuneko abiadurara jotzen du igarotako denbora tarteak zerorantz jotzen duenean. Hau da:

Ikuspegi fisiko batetik aldiune jakin bateko abiadura kalkulatzeko, nahikoa izango litzateke une jakin batean higikariaren posizio bektorea eta ezagutzea, eta hurrengo une batean (geroz eta txikiagoa izango dena, noski) lortutako posizio bektorearen arteko diferentzia aurkitzea. Lortutako bektorea igarotako denbora tartearekin zatituko genuke eta lortutako adierazpena aldiuneko abiaduratik oso gertu egongo den abiadura izango da. Prozesu hau etengabe errepikatuz gero, aldiuneko abiaduraren balioaren hurbilketa bat egitea lortuko genuke.

Halere, aurreko adierazpen matematikoari irtenbidea emateko badaukagu aukera eragiketa matematiko berri bati heltzeko: hau da, goiko adierazpen horren balio matematiko zehatza aurkitzeko nahikoa da desplazamendu bektorearen denborarekiko deribatua kalkulatzea.

Hona hemen goiko adierazpena egiaztatzen duen adibide bat.

Kontutan izanda posizio bektorearen adierazpena bere osagai intrintsekoen baitan:

Deribatuen propietateetan oinarriturik:

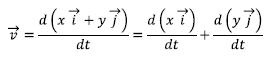
Beraz, aldiuneko abiadura bektorea osatzen duten osagaiak kalkulatzeko, nahikoa da posizio bektorearen osagaietako bakoitza denborarekiko deribatzea. Horrela lortuko dugu aldiuneko abiadura bektorearen adierazpen analitikoa:

Beraz:

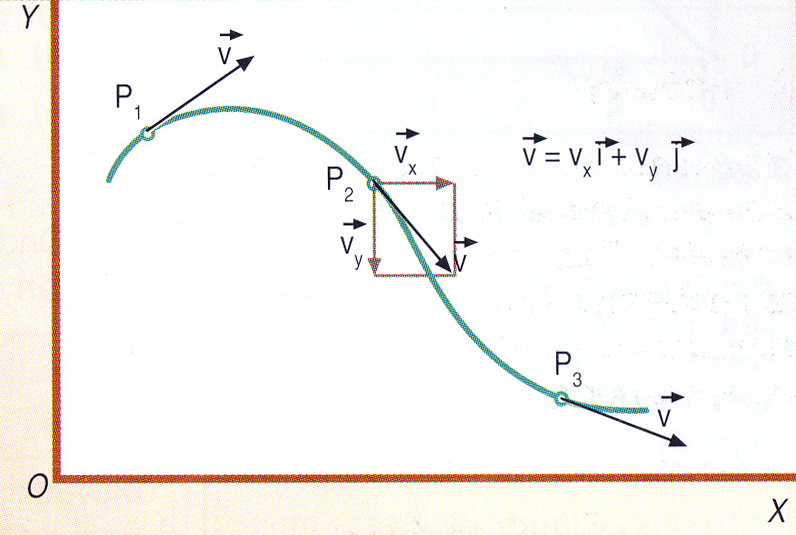
Garbi dago, beraz, aldiuneko abiadura ere magnitude bektoriala dela. Defini dezagun:

• MODULUA: edozein bektore baten modulua bezala kalkula daiteke. Kasu honetan:
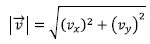
• NORABIDEA: irudian garbi ikus daitekeenez, denbora tartea txikitzen goazen heinean, batezbesteko abiadura ibilbidearen tangetearekin bat dator. Horixe izango da, berz, aldiuneko abiaduraren norebidea; desplazamendu bektorearekin bat etorriko da eta ibilbidearekiko ukitzailea izango da.
• NORANTZA: desplazamendu bektorearekin bat etorriko da.

Arintasuna edo bizkortasuna

Aurrean aipatutako egoera “limite” horretan, desplazamendu bektorearen modulua, , ibildearen balioarekin, , bat datorrela esan daiteke. Hau da, denboraren aldaketa infinitesimal batentzat, , eta ondorioz:

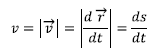
Kontutan izan magnitudearen balioa eskalarra dela. Goiko adierazpenean ikusten den bezala bere balioa bat dator abiadura bektorearen moduluarekin, eta bizkortasun edo arintasun izenez ezagutzen da.

Esan dugunaren arabera, aldiuneko abiadura ibilbidearekiko ukitzailea da beti. Ondorioz, abiaduraren adierazpen bektoriala beste era batera ere eman daiteke: bere modulu eta aldiuneko abiaduraren norabide eta noranzko bera duen izeneko bektore unitarioren biderketa bezala. Beraz:

Ebaztutako Ariketa

1.- Plano batean dagoen partikula baten posizioa ondorengo ekuazio bektorialaren bitartez adierazten da:

1. Aurkitu ezazu partikularen posizioa t=1 s eta t=2 s-etan
2. Zein izan da bitarte horretan higikariak eraman duen batezbesteko abiadura?
3. Zein da higikariaren abiadura t=1 s unean? (Ebazpena, pdf-503 KB)

Proposatutako Ariketak

2.- Deribatuaren kontzeptua erabili gabe, esplikatu ezazu zeri deitzen diogun ibilbidearen puntu bateko higikariaren aldiuneko abiadura.

3.- Bi gorputzek denbora berean desplazamendu bera egiten badute, hau baieztatu ahal da:

1. Bukaerako abiadura berdina izango dutela
2. Hasierako abiadura berdina izango dutela
3. Batez besteko abiadura berdina izango dutela

4.- Plano batean dagoen partikula baten posizioa ondorengo ekuazio bektorialaren bitartez adierazten da:

Higiduraren magnitudeak SIn adierazten badira, kalkulatu:
1. Higikariaren posizioa t=2 s eta t=3 s denbora uneetan
2. Denbora tarte horretan izandako batezbesteko abiadura
3. Aldiuneko abiadura.
4. Egin ezazu higiduraren deskribapen orokorra: zein higikariak deskribatzen duen ibilbide mota, nondik hasten den higidura, nola aldatzen dira abiadura eta azelerazioa….. Hau da, egizu HIGIDURAREN DESKRIBAPEN FISIKOA.

5.- Higikari bat lerro zuzen batean zehar desplazatzen da  ekuazioaren bitartez, non t-k denbora adierazten duen segundotan.Zera galdetzen da:

1. Zein denbora unetan aldatzen du higikariak bere mugimenduaren norantza?
2. Zein posiziotan aurkitzen da une horretan?
3. Zenbat balio du bere abiadurak une horretan?