Higiduraren deskribapena

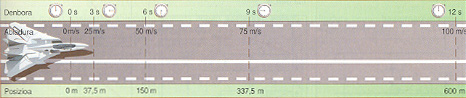
Irudian ikus daiteken bezala, higikariaen abiaduraren norabide eta noranzkoak denborarekiko konstanteak dirauten bezala, bere modulua kantitate konstante batean handitu edo txikitzen da. Horrexegatik daukagu higidura zuzen eta uniformeki azeleratu bat.

Lehen ikusi dugun bezala, ibilbide zuzena duen higikari batek ez du bere norabidea aldatzen eta, ondorioz, higidura horretako azalerazioaren osagai normala zero da.

Beraz, higikari baten ibilbidea zuzena denean eta abiaduraren balioa aldatzen denean, bere higidurak azelerazioaren osagai tangentziala bakarrik izango du. Gaitera, denborarekiko era proportzionalean aldatzen denez, bere balioa konstantea izango da. Kasu horretan, azelerazio tangentziala eta azelerazio osoa bat etorriko dira.

Beraz, HZUAn:

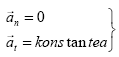Ondorioz: =konstantea

Higidura zuzen uniformeki azeleratuaren berezitasuna azelerazioaren osagai tangentziala konstantea dela eta bere balioa azelerazio osoarekin bat datorrela.

Higiduraren Ekuazioak

1) v(t) ekuazioa

Higidura mota honetan azelerazioaren balioa konstantea denez, batezbesteko azelerazioa eta aldiunekoa berdinak izango dira:

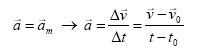
Adierazpen horretatik askatzen badugu:

Higidura zuzen uniformean egin dugun moduan, hemen ere higidura zuzena denez, erreferentzi sistema modura, higiduraren norabide bereko OX ardatza har dezakegu. Horrela eginda, bektore guztiek izango dute norabide hori berori, eta abiaduraren eta posizioaren ekuazioak era eskalarrean adierazi ahal izango dira.

, eta ondorioz:

Hainbat baldintzapean, ekuazio honek itxura desberdinak har ditzake:

1. Higidura zuzen uniformean bezala, hemen ere denboren jatorria aukeratu dezakegu. Eta t₀=0 izaten saiatzen bagara, lortuko dugu:
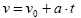
2. Horrez gaitera, higikaria geldiunetik abiatzen bada HZUAz, kasu horretan v₀=0 izango da eta ondorengo adierazpena erabiliko dugu:

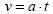
2) x(t) ekuazioa

Higidura mota honetan abiadura uniformeki aldatzen denez, batezbesteko abiadura bektorea hasierako eta amaierako abiadura bektoreen baturaerdi modura adierazi genezake:

Bestalde, batezbesteko abiadura bektorea definizioaren arabera:

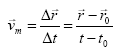
Bi adierazpen hauek berdinduz:

Gainera, aurreko atalean lortutako abiaduraren ekuazioa erabiliz:

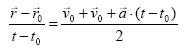
Ondorengo ekuazioan eragiketak eginez eta  bakanduz:

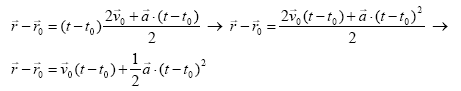
Azkenik:

Jada, aurrean behin baino gehiaton errepikatu den bezala, erreferentzi sistematzat ibilbide zuzenarekin kointziditzen duen OX ardatza hartuko dugu. Bestalde, higidura zuzena izateagatik ekuazio horretan parte hartzen duten bektoreek norabide bera izango dute. Gainera t₀=0 dela suposatzen badugu, x(t) ekuazioa ondorengoa izango da:

(A)

Higiduraren grafikoak

Kasu honetan ere, posizio, abiadura eta azelerazioaren aldakuntza denborarekiko dagozkien grafikoak aztertuko ditugu. Grafiko hauen interpretazio egokia ezinbestekoa da higidura bakoitzaren ezaugarri orokorrak ondo ulertzeko

• a/t grafikoa:

Azaldu dugunez, azelerazio konstantea duen higidura bat aztertzen ari gara. Beraz, funtzio konstante baten aurrean gaude.

• v/t grafikoa:

HZUn r(t) funtzioaren baliokidea da v(t) funtzioa.

HZU:

HZUA:

Beraz, funtzio afin batetaz ari gara. HZUn bezala, zuzenaren ezaugarri orokorrak ekuazioan agertzen diren magnitude ezberdinen ikurren araberakoa izango da. Beraz, ondo aztertu beharko ditugu v, v₀ eta a parametroak eta ondoren higidura interpretatu.

• x/t grafikoa:

Posizioaren aldaketa denborarekiko bigarren mailako ekuazio baten bitartez adierazten denez, x(t) funtzio parabolikoa izango da. Parabola horren itxura, berriro ere, funtzioan agertzen diren magnitude ezberdinen menpekoa izango da, x₀, v₀ eta a magnitudeek dituzten balio eta zeinuaen araberakoak, alegia.

Kontutan Hartzekoak

A) Hirugarren ekuazio bate ere ondoriozta dezakegu HZUAren kasurako, abiadura eta posizioa erlazionatuz. Ekuazio hori lortzeko, lehenik denbora askatuko dugu abiaduraren ekuaziotik eta ondoren balio hori posizioaren ekuazioan ordezkatuko dugu, honako emaitza hau lortuz:

Proposatutako Ariketak

5.- Higidura uniformeki azeleratua duen higikari batek hasierako abiadura negatiboa du. Bere gain agertzen den azelerazio konstanteak ikur negatiboa izanik ere, egizu higidura adierazten duen v/t grafikoa. Ziurta al daiteke higikaria poliki-poliki gelditzen ari dela?

6.- Ondorengo grafika hauetatik esan zein den egokia ondoren aipatutako mugimenduentzat: (TW26)

1. Geldiunetik abiatuz 2 m/s-ko abiaduraz eta azelerazio konstantez higitzen den moto baten mugimendua
2. Abiadura konstantez 2 m egiten dituen kotxe baten mugimendua
3. Hasieran 2 m/s-ko abiaduraz mugitzen den eta uniformeki balaztatuz gelditzea lortzen duen txirrindulari baten mugimendua
4. Higidura zuzen eta uniformeki azeleratuz 2 m korritzen dituen ume baten mugimendua

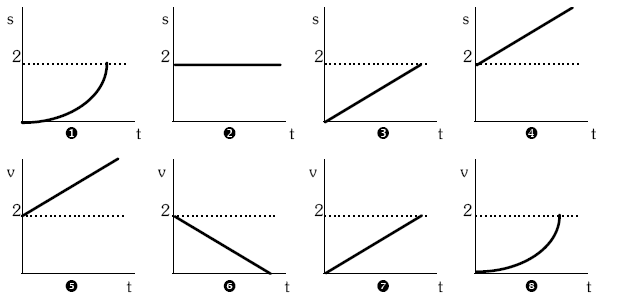
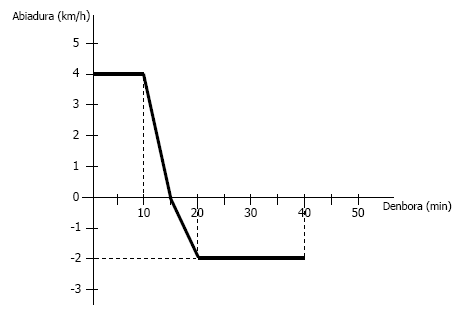
7.- Txano-Gorritxoren gurasoek neskatoa amonaren etxera joaten ez delaren errezeloa dute. Susmo txar hauek konfirmatzeko asmoz, bere saskitxoan, madalenen artean ezkutatuta, abiaduraren balioa eta norabidea jasotzen duen neurgailu bat ipini diote. Tramankulu honetatik lortzen diren datuen interpretazio grafikoak (ikus azpian) garbi konfirmatzen du etxekoen susmo txarrak. Egiaztatu ezazu zuk zeuk, jakinik Txano-Gorritxoren etxetik amonaren etxera 1 km-ko distantzia dagoela. Amonaren etxetik baino zenbat metro lehenago geratu da?. Egiaztatu ezazu, berriro ere etxera bueltatzen dela.

8.- 90 km/h-ko abiadura daraman kotxe batek 100 m-ra dagoen kotxe bat aurreratzera doa.

1. Aurreratu behar duen kotxea geldirik badago, zein izango da aurreratze honetan eraman duen azelerazioa eta behar izan duen denbora, 126 km/h-ko abiadura lortzen badu?.
2. Aurreratu behar duen kotxea 36 km/h-ko abiadura uniformez higitzen bada aurrekoaren norabide eta norantza berean, zenbat denbora beharko du kotxe hau aurreratzeko a) atalean kalkulatu duzun azelerazio berarekin higitzen bada?