Higiduraren deskribapena

XVII. mendearen hasieran, Galileok gorputzak jausten zuten higidura aztertu zuen. Higidura hori aztertzeko, Pisako dorre makurretik masa eta itxura desberdineko gorputzak erortzen uzten omen zituen eta esperimentu batetik bestera gauza horien itxura eta jausten uzteko altuera aldatzen omen zituen.

Esperimentu horien ondorioz, Galileok gorputz batek erortzean egiten duen distantzia eta erortzeko behar izan duen denboraren karratua zuzenean proportzionalak direla frogatu zuen. (A)

Horrek esan nahi du gorputz baten erorketa higidura zuzen uniformeki azeleratua dela. Erorketa hau gorputzen gainean eragiten duen indar grabitatorioaren ondorioa izango da. Beraz, gorputzek erortzean hartzen duten azelerazioa grabitatearen azelerazioa  da, eta beherantz zuzenduta dago, Lurraren zentrorantz. (B)

Datorren urtean, Lurraren eremu grabitatorioa aztertzen dugunean ikusiko duzunez, grabitatea (eremu grabitatorioaren intentsitatea da bere izen zehatza) Lurraren eremu grabitatorioak eragiten duen indarra masa unitatearekiko da, hau da, eremuaren intentsitatea adierazten du. Bere balioa konstantea da eta, aurrean esan bezala, lur-gainazalean eta lur-gainazaletik gertu, bere balioa 9,8 N/kg ingurukoa dela onar daiteke.

Higiduraren ekuazioak

Esan dugun bezala, lur-gainazalarekiko perpendikularrak diren higidurak (erorketak nahiz gorakako jaurtiketak) higidura uniformeki azeleratuak dira, higikarien gainean eragiten duen azelerazioa konstantea delako (g=9,8 m·s^-1). Beraz, higiduraren ebazketa eta interpretazioa egiterakoan erabiliko ditugun ekuazio matematikoak eta grafikoak aurreko atalean zehaztutakoen berdinak izango dira. Halere badira aintzat hartu beharreko puntu bi:

1. Gorputzaren desplazamendua erreferentzi sistemarekiko:

Lur-gainazaletik ematen diren higidura zuzenentzat erreferentzi sistema OX ardatzarekin kointzidiarazi dugu, posizioarentzat erabilitako ikurra izanik. Kasu honetan, higidura ardatz horrekiko perpendikularra denez, desplazamendua OY ardatzean zehar ematen dela onar daiteke. Bai gorputzaren abiadura baita azelerazioa ere norabide berekoak izango dira. Hori dela eta, ekuazioetan sinbologia aldaketa txiki bat egin beharko dugu:



Bestalde, oso arrunta izaten da horrelako planteamenduetan gorputzak lortzen duen altueraz hitz egitea. Noranzkoaren aldaketarik ematen ez bada, gorputzaren posizioa bat dator jaurtiketaren jatorriarekiko lortzen duen altuerarekin. Horregatik y=h egiten da kasu askotan.

2. Zeinuen irizpidea aukeratutako erreferentzi sistemarekiko:

Atal honekin kontu pixka bat izan behar da. Aurreko gaian adierazi dugun bezala higikariaren desplazamenduan bere posizioa zehazteko erreferentzi sistemaren jatorria nahi dugun espazioko puntuan ipini dezakegu. Honen arabera lortuko ditugun ekuazioen “itxura” desberdina izan arren, denek adieraziko dute higidura mota berdina.

Esan bezala, gure kasuan desplazamenduaren norabidea OY ardatzarekin koinziditu araziko dugu. Halere, gorputz baten erorketa aztertzerakoan, erreferentzi sistemaren jatorria higiduraren jatorriarekin kointzidiarazi dezakegu, edota erreferentzi sistemaren jatorria lur-gainazalean bertan koka daiteke. Esan bezala kasu baten edo bestean higidura bera izango da, noski, baina erabiliko ditugun magnitudeen zeinuak ezberdinak izango dira kasu batean edo bestean.

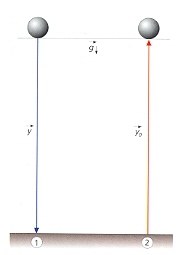1. Erreferentzi sistemaren jatorria higiduraren jatorrian kokatzen bada, erorketaren noranzkoa positiboa dela suposatuz: (ikus 1. irudia)
• Posizioa: posizio bektorea, beherantz doanean, positiboa izango da.
• Abiadura: jatorri puntutik beherantz higitzen denean positiboa eta gorantz doanean negatiboa
• Azelerazioa: grabitatea ere beherantz zuzendurik dagoenez, bere zeinua positiboa izango da.
2. Erreferentzi sistemaren jatorria lur-gainazalean kokatzen bada, goranzko norabidea positiboa dela suposatuz: (ikus 2. irudia)
• Posizioa: bektore positiboa izango da lur-gainazalaren gainean kokatuta gaudenean.
• Abiadura: positiboa da norabide gorakorra denean eta negatiboa da gorputza beheraka datorrenean
• Azelerazioa: negatiboa da beti, Lurraren zentrorantz zuzenduta dagoelako

Aurrekoaren arabera, ondorengoak izango dira erorketa libre nahiz jaurtiketa bertikaletan (gorantz nahiz beherantz) agertuko zaizkigun ekuazioak:

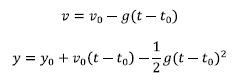
Kasu bakoitzean ondo aztertu planteatutako egoeran zeintzuk diren magnitude ezberdinen ikurrak eta ondoren ekuazioetan ordezkatu.

Higiduraren grafikoak

Higidura bertikala HZUA izanik, topatuko ditugun adierazpen grafikoak jadanik ezagunak izango ditugu. Hori bai, garbi izan beharko dugu, aurrean adierazi den bezala, zein izango den magnitude bakoitzaren ikurra. Horren arabera, grafiko bakoitzak itxura propioa izango du.

Kontutan hartzekoak

A) Egia esanda gorputzen erorketa higidura uniformeki azeleratuarekin ematen dela onar daiteke soilik HUTSEAN. Lur-gainazalera gertatzen diren erorketetak , berez, ez dira uniformeki azeleratuak, izan ere, airearen ondorioz gorputzen gainean marruskadura indar agertzen da, berau, gorputzen bolumenarekin, formarekin eta erorketan daramaten abiadurarekin erlazionaturik dagoelarik.

B) Lurrak bere gainazaletik hurbil dauden gorputzei eragiten dien erakarpenaren ondorioz, azelerazio grabitatorioa sortzen da.

Lurraren eremu grabitatorioa aztertzean ikusiko duzunez, grabitatearen azelerazioa, g, txikiagotu egiten da Lurraren zentrotik urrundu ahala.

Nolanahi dela, Lurraren gainazaletik metro gutxira gertatzen diren higiduren kasuan, g-ren balioa konstantea dela suposa dezakegu, 9,8 m·s^-2-ko baliokoa, zeren horrela eginda errore oso txikia egiten baitugu.

Bestalde, gorputzen higidura bertikala hutsean gertatzen denean soilik da HZUA motakoa. Atmosferan gertatzen denean, airearen marruskadurak balaztatu egiten du gorputzen higidura. Hala ere, azalpenak sinplifikatzeko, arbuiatu egingo dugu airearen erresistentzia.

Gehiago Jakiteko

Newtonen grabitazio unibertsalaren legea

Lurraren eremu grabitatorioaren menpe dauden gorputz guztiak, grabitatearen indarraren menpe egoten dira. Newtonen Grabitazio Unibertsalaren legearen kasu berezi bat da, non bertan Lurraren masaren eta gorputzen masaren arteko interakzioa bakarrik aintzat hartzen diren (datorren urtean ikasiko dugun bezala). Gorputzaren gainean Lurraren eremu grabitatorioak eragiten duen indarrak norabide bertikala du (egokiago esanda zentrala, hau da, Lurraren zentroa eta gorputza lotzen dituen zuzenarena), noranzkoa beherantz (Lurraren zentrorantz) eta bere balioa konstantea dela kontsidera daiteke (Lurraren gainazalarekiko puntu hurbiletan ari bagara behintzat).

Gorputzen erorketa askearen adibide grafikoa

Azpiko bideoan Atlantis transbordadorearen erregai depositu baten erorketa askea nola ematen den ikus dezakezue. Bideoak depositua askatu eta itsasora erori arteko denbora tartea adierazten du. Kontutan hartu erorketa osoan, gorputzaren gainean agertzen den azelerazio bakarra grabitatearena dela.

Proposatutako ariketak

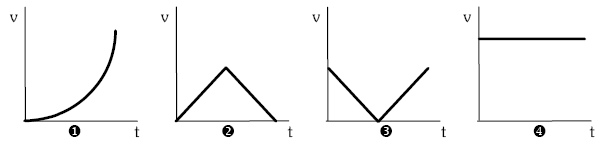
9.- Lurrean zaudela harri bat jaurtitzen duzu gorantz eta denbora bat pasa ondoren lurrera bueltatzen da. Grafiko hauetatik zeinek adierazten du egokien harriaren abiaduraren moduluaren aldaketa?. Arrazoitu ezazu zure erantzuna.

10.- Altzairuzko bola txiki batek 3,5 s behar izan ditu 80 m-ko altuera batetik erortzeko. Justifika ezazu bolatxoak hasierako abiadurarik ba ote zuen edo ez erortzen hasi denean. Erantzuna baiezkoa bada, aurkitu ezazu hasieran eman zaion abiaduraren balio hori eta, ezezkoa bada, kalkula ezazu zein izango den lurra ukitzerakoan izango duen abiadura.(TW210)

11.- Etxe baten teilatutik erortzen uzten den harri batek 0,25 s behar du 2,7 m-ko luzera duen leiho batetik igarotzeko. Kalkulatu leihoaren goiko ertzetik teilatura dagoen distantzia.

12.- Harri bat gorantz jaurtitzen da 25 m/s-ko abiaduraz, lurra baino 20 m gorago dagoen etxe baten goialdetik. Aldi berean, lurretik beste harri bat jaurtiki da gorantz 30 m/s-ko abiaduraz. Kalkula itzazu:

1. Lurretik zein distantziara gurutzatuko diren eta zenbat denbora pasatu den gurutzatu arte
2. Aldiune horretan harri biek izan duten abiadura