Azter dezagun jarrain zernolako interferentzia mota ematen den bi foku koherente lotzen dituen zuzeneko edozein puntutan.

Uhin geldikorrak abiadura berean, norabide berean eta aurkako norantzan aurrera egiten duten bi uhin sinusoidal berdin interferitzen dutenean sortzen dira (ikus ondorengo appletak: I eta II).

Gainezartzen diren uhinak bakarka aztertzean puntu guztiek anplitude berberarekin bibratzen dutela ikus daiteke. Baina gainezartzean sortzen den uhin geldikorraren puntu bakoitzaren anplitudea jatorriarekiko duten posizioaren arabera dago. Puntu batzuk jatorrizko anplitudearen bikoitzarekin bibratzen dute (sabelak) eta beste batzuk geldi daude (nodoak).

Lau irudien artean T/4-eko denbora tartea dago. Ikusten denez, ondoz ondoko bi nodoen artean jatorrizko uhinen uhin-luzeraren erdiko distantzia dago.

Uhin geldikorrak ezin dira zehazki uhin higidurak bezala kontsideratu ez bait da energia garraiorik ematen ingurunean zehar. Inguruneko puntu bakoitzak (nodoak ezik) osziladore harmonikoak izango balira bezala bibratzen dute, bakoitza bere anplitudearekin eta bakoitza bere energia mekaniko bereizgarriarekin. Nodoetan, berriz, Em=0 izango da. Energia balio ezberdinak izanik, garbi dago energia mekanikoaren garraiorik ez dela ematen eta, ondorioz, uhinaren perfila ez da desplazatzen, geldikorra da.

Uhin geldikor baten ekuazioa lortzeko, jatorritik x distantziara dagoen puntu batentzat, interferentzi uhinen ekuaziotik abiatuko gara, hauetako batek ibilitako distantzia bestearen aurkako norantzan ematen delarik.

eskuinera doanarentzat.

ezkerrera doanarentzat.

Gainezarmen printzipioa aplikatuz elongazio ordezkaria aurkituko dugu:

Aurreko atalean ikusitako erlazio trigonometrikoa aplikatuz:

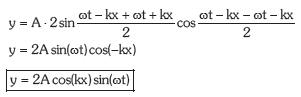
adierazpena denborarekiko askea da eta puntu bakoitzaren anplitudea ematen digu. Bere balioa kontsideratzen den puntuaren x abzisaren funtzioan dago.

Anplitudearen balio maximoa aurkitzeko zera gertatu behar da:

Edota: , n=0,1,2… izanik

Abzisaren balioa uhin-luzeraren laurdenaren kopuru bikoitia denean maximo edo sabelak izango ditugu.

Anplitudearen balioa minimoa izango da ondorengo baldintza betetzen duten puntuetan:

Beraz: 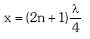, n=0,1,2… izanik.

Abzisaren balioa uhin luzeraren laurdenaren kopuru bakoitia denean minimo edo nodoa izango dugu.

Bi sabelen arteko distantzia n-ri elkarren segidako bi balio emanez aurki daiteke. Honela ohar gaitezke elkarren arteko distantzia λ/2 dela, nodoekin gertatzen den bezala.

Ebaztutako Ariketa

17.- y₁=6sin(1500t+250x) eta y₂=6sin(1500t-250x) ekuaziodun bi uhin (unitateak S.I.-an) interferitzen dira.

Kalkulatu:

1. Uhin geldikorraren ekuazioa.
2. Anplitudea nodoetan.
3. Segidako bi sabelen arteko distantzia.(Ebazpena, pdf-30kb)

Proposatutako Ariketak

18.- ekuazioak, unitateak Sistema Internazionalean, uhin geldikor bat adierazten du.

1. Zeintzuk dira aurkako norantzan bidaiatuz interferitzen direnean uhin geldikor hau eragiten duten bi uhin koherenteen uhin-luzera, maiztasuna eta anplitudea?
2. Uhina sortu den ingurunearen mugak x=0 eta x=18 m badira, kalkulatu nodo eta sabelen posizioak.
3. Nola aldatzen da x=2 m puntuan dagoen partikularen abiadura denborarekiko?.

19.- Uhin baten ekuazioa honako hau da:, x eta y m-tan eta t segundotan neurtu direlarik. Zehaztu:

1. Zein uhinekin interferitu behar du uhin geldikor bat eragiteko?
2. Zein da uhin geldikor ordezkariaren ekuazioa?
3. Bi fokuak elkarrengandik 1 m-ra aurkitzen badira, zenbat sabel agertuko dira?