Higidura zirkularra ibilbide zirkularra irudikatzen duen puntu batek egiten duena da.
Higidura mota hau daukaten adibide asko ditugu: automobil baten gurpila, biraka dabiltzan DVDak edo baita arropa garbigailu baten danborra.
.jpg) Aurreko ataletan aztertutako higidura guztiak zuzenak izanik, higikariak buruturiko distantziaren kalkulua egiteko arazo gehiegirik ez genuen izan. Higidura zirkularrean, ordea, higikariak ibilitako espazioa, biraketa ardatzetik aurkitzen deneko distantziaren araberakoa da. Hau da, jo dezagun birak ematen dituen gurpil bat. Gurpilak bira oso bat burutzen duenean, garbi dago pneumatikoaren azalean dagoen partikula batek eginiko ibilbidea eta ardatzetik gertu dagoen gurpileko torloju batek egiten duena oso desberdinak direla. Hori bai, biek deskribatuko dute angelu bera denbora tarte berdinean.
Aurreko ataletan aztertutako higidura guztiak zuzenak izanik, higikariak buruturiko distantziaren kalkulua egiteko arazo gehiegirik ez genuen izan. Higidura zirkularrean, ordea, higikariak ibilitako espazioa, biraketa ardatzetik aurkitzen deneko distantziaren araberakoa da. Hau da, jo dezagun birak ematen dituen gurpil bat. Gurpilak bira oso bat burutzen duenean, garbi dago pneumatikoaren azalean dagoen partikula batek eginiko ibilbidea eta ardatzetik gertu dagoen gurpileko torloju batek egiten duena oso desberdinak direla. Hori bai, biek deskribatuko dute angelu bera denbora tarte berdinean.
Hori dela eta, higidura zirkularretan translazioarekin zerikusia duten magnitudeak alde batera utzi eta errotazioarekin zerikusi zuena dutenak aztertuko ditugu. Magnitude hauei magnitude angeluarrak deritze.
Magnitude angeluarrak
 Batezbesteko abiadura angeluarra (ωm): biraturiko angeluaren,
Batezbesteko abiadura angeluarra (ωm): biraturiko angeluaren, ![]() , eta pasaturiko denboraren,
, eta pasaturiko denboraren, ![]() , arteko zatidura da.
, arteko zatidura da.
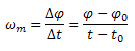
Sistema Internazionalean radian segundoko (rad/s) unitateetan adierazten da.
Aldiuneko abiadura angeluarra (ω): batezbesteko abiadura angeluarraren balioa da, pasaturiko denborak zerorantz jotzen duenean.
![]()
Batezbesteko azelerazioa angeluarra (αm): abiadura angeluarraren aldakuntzaren eta pasaturiko denboraren arteko zatidura da.
![]()
Sistema Internazionalean radian segundo karratuko (rad/s2) unitateetan adierazten da.
Aldiuneko azelerazio angeluarra (α): batezbesteko azelerazio angeluarraren balioa da, pasaturiko denborak zerorantz jotzen duenean.
![]()
Higidura zuzena eta zirkularraren arteko erlazioa
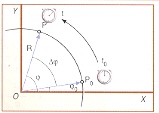
.jpg) Alboko irudian ikus daitekeenez, zirkunferentziaren arkuaren luzera, ∆s, eta horren angelua,
Alboko irudian ikus daitekeenez, zirkunferentziaren arkuaren luzera, ∆s, eta horren angelua, ![]() (radianetan neurtua), erradioaren bidez erlazionatzen dira:
(radianetan neurtua), erradioaren bidez erlazionatzen dira:
![]()
Adierazpen hau ∆t gaiaz zatituz, honako hau lortuko dugu:
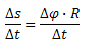
![]() egitean, limitean ondorengo adierazpena lortzen dugu:
egitean, limitean ondorengo adierazpena lortzen dugu:

Kurbadura erradioa denborarekiko konstantea izanik higidura zirkularraren kasurako:
![]()
Eta ondorioz:
![]()