Azpiko irudian bi txakurrek eginiko  eta  indarrez herrestan eramandako lera bat ikus dezakegu.

Sorturiko efektua,  indarra egingo lukeen txakur bakar batek sortuko lukeenaren baliokidea da. Indar hori beste bien batura bektoriala da eta indar erresultantea deritzogu, edo huts-hutsean, erresultantea.

Gorputz baten gainean eragiten ari den indar-sistema baten erresultantea, 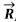, sistemako indar guztien batura bektoriala da.

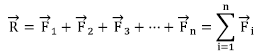
Solido zurrunean eragiten ari den indar-sistemaren erresultantearen kalkuluari, indarren konposizioa deritzo. (A)

Indar konkurrenteen konposizioa

Indar konkurrenteak, puntu batean elkar ebakitzen duten lerro zuzenetan aplikaturikoak dira.

Indar konkurrenteen sistema baten indar erresultantea kalkulatzean, indar guztiak solidoaren puntu berean aplikatzen direla suposatzen da.

Ikus dezagun nola determinatu indar erresultantea, indar konkurrenteen norabide eta noranzkoaren arabera.

1. Norabide eta noranzko bereko indarrak
• Modulua: sistemako indarren moduluen batura.
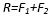
• Norabidea: indar osatzaileen norabide berbera
• Noranzkoa: indar osatzaileen noranzko berbera
• Aplikazio-puntua: indar osatzaileen puntu berbera
2. Norabide bereko eta aurkako noranzkoko indarrak
• Modulua: sistemako indarren moduluen kendura.
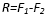
• Norabidea: indar osatzaileen norabide berbera
• Noranzkoa: modulu handieneko indarraren noranzkoa
• Aplikazio-puntua: indar osatzaileen puntu berbera
3. Norabide perpendikularreko indar konkurrenteak

Paralelogramoaren arauaz determinatzen da. Bektore bakoitzaren muturretik beste bektorearen paraleloa marraztu, eta horrela bi paraleloen ebakidura-puntua lortuko dugu.

• Modulua: Pitagorasen teorema aplikatuko dugu.
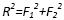
• Norabidea eta noranzkoa: trigonometriako oinarrizko arrazoietatik abiatuz: 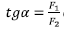 eta ondorioz,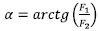
• Aplikazio-puntua: indar osatzaileen puntu berbera.
4. Norabide desberdineko indar konkurrenteak

Kasu honetan ere paralelogramoaren arauz determinatu ahal izango dugu erresultantea. Hala ere, ebazketa matematikoa kasu honetan zerbait konplexuagoa bilakatzen da.

Indar erresultantearen kalkulu analitikoa egiteko (hau da, bere modulu, norabide eta noranzkoa zehazki determinatzeko), emandako bektoreak norabide perpendikularrak izango dituzten osagaietan deskonposatu beharko ditugu, eta ondoren, aurrean aipatutako arauak jarraituz, erresultantea kalkulatu.

Hona hemen adibide grafiko bat:

 eta  indarrak X eta Y ardatzetan proiektatzean,

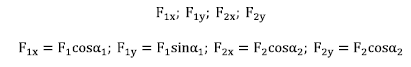
Erresultantea eta indarren batura bektoriala da:

Honela, ba, indar erresultante bektorearen osagaiak honako hauexek dira:

• Modulua: Erresultantearen modulua hauxe da:
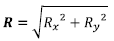
• Norabidea eta noranzkoa: Erresultanteak horizontalarekin osatzen duen angelua era honetan lor daiteke:
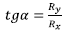
• Aplikazio-puntua: indar osatzaileen puntu berbera.

Indar paraleloen konposizioa

Indar paraleloak norabide paraleloak dituztenak dira.

Ikus dezagun nola determinatu indar erresultantea kasu honetan:

1. Noranzko bereko indar paraleloak

• Modulua: sistemako indarren moduluen batura.
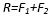
• Norabidea: indar osatzaileen norabide berbera
• Noranzkoa: indar osatzaileen noranzko berbera
• Aplikazio-puntua: ondoko erlazioaren bidez dago determinaturik: 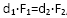, kontutan izanik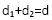 
1. Aurkako noranzkoko indar paraleloak

• Modulua: sistemako indarren moduluen kendura.
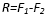
• Norabidea: indar osatzaileen norabide berbera
• Noranzkoa: modulu handieneko indarraren noranzko berbera
• Aplikazio-puntua: ondoko erlazioaren bidez dago determinaturik: 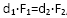, kontutan izanik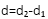 

Bi indar paraleloren aplikazio-puntua grafikoki ere kalkula daiteke, bai indarrak noranzko berekoak diren kasuan, baita aurkako noranzkokoak diren kasuan ere.

Aplikazio-puntua lortzeko, ondoko pausoak emango ditugu bi kasuetan:

• Indar baten aplikazio puntutik abiatuz, 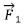-en B puntutik adibidez, 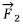-ren paraleloa den segmentu bat marraztuko dugu, norantza berean eta luzera berekoa. Horrela, C puntua lortuko dugu
• Beste indarraren aplikazio-puntutik, A puntutik, 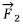-ren paraleloa den segmentu bat marraztuko dugu, luzera berekoa, baina aurkako norantzan. Horrela, D puntua lortuko dugu.
• C eta D puntuak lerro zuzen batez bilduko ditugu. Zuzen honek O puntuan ebakiko du A-tik eta B-tik pasatzen den zuzena. Puntu hori da, hain zuzen, erresultantearen aplikazio-puntua.

Kontutan hartzekoak

A) Indar erresultante kontzeptua solido zurrunen kasuan aplikatzen da soilik; hain zuzen, horietan indar-sistemen eragina pausagune edo higidura-egoera aldatzean datza, eta ez deformazioa sortzean.

Proposatutako ariketak

1.- Gorputz batean bi indar aplikatu dira norabide berean. Nolakoak izan behar dute indarrek, gorputzak geldi iraun dezan?. Ondo esplikatu.

2.- Aplikazio puntu bera duten bi indarren moduloa 10 eta 15 N-ekoak badira, aurkitu ezazu indar hauen erresultantea ondorengo kasuetan:

1. 0º angelua osatzen dutenean.
2. 45º angelua osatzen dutenean.
3. 90º angelua osatzen dutenean.
4. 120º angelua osatzen dutenean.
5. 180º angelua osatzen dutenean.

3.- Modulo bereko bi indar ( eta ) abzisa ardatzarekiko osatzen duten angeluak 45º eta 135º-koak dira. INONGO KALKULURIK GABE, arrazoitu ezazu zein izan beharko den falta den indarraren modulo, norabide eta norantza hiruen indar ordezkaria nulua (  =0) izan dadin. ONDO ESPLIKATU. (TW303)

4.- Aurkitu ezazu grafikoan adierazten diren indarren ordezkaria:

5.- 4 m-ko luzera duen enbor baten muturretan bi indar paralelo eta norantza berekoak egin dira, enborrarekiko norabide perpendikularrean, 20 N eta 45 N-ekoak.

1. Marraz ezazu indar-sistema
2. Determina ezazu erresultantearen modulua eta aplikazio puntua

6.- Gorputz batean 50 N eta 20 N-eko bi indar aplikatzen dira.Determina itzazu erresultantearen modulua, norabidea, norantza eta aplikazio puntua ondorengo kasuetan:

1. Aplikazio-puntu, norabide eta norantza bera dutenean.
2. Aplikazio-puntu eta norabide bera baina aurkako norantza dutenean.
3. Indarrak paraleloak badira, norantza berekoak eta aplikazio-puntuen arteko distantzia 3 m-koa denean.
4. Indarrak paraleloak badira, aurkako norantzakoak eta aplikazio-puntuen arteko distantzia 3 m-koa denean.