Demagun a eta b dimentsioko espira errektangeluarra indukzioko eremu magnetiko uniformearen barruan dagoela.

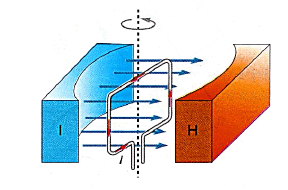
Gainera eremu magnetikoaren bektoreak eta gainazal bektoreak Ï• angelua osatzen dute. Espiratik I intentsitateko korronte elektrikoak zirkulatzen du.

Espiraren alde bakoitza eroale zuzentzat har dezakegu eta, ondorioz, Laplacen legea aplika daiteke.

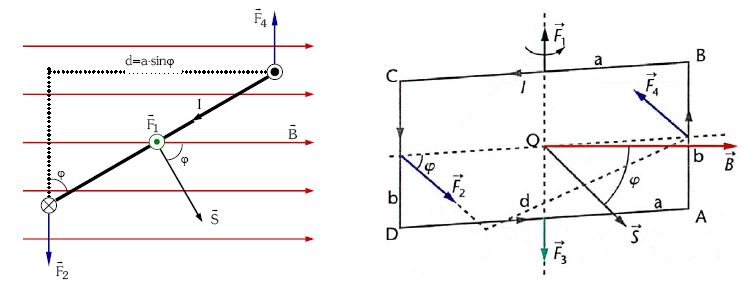
Lortuko ditugun emaitzak ondorengoak dira:

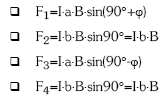
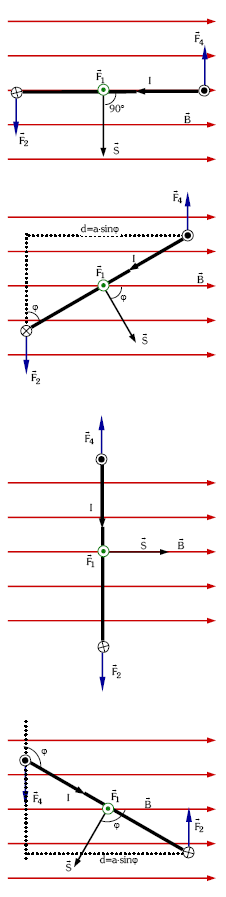Ikusten denez, BC eta DA eroaleetatik doan korrontearen elkarrekintzari dagozkien F₃ eta F₁ indarrek elkar ezeztatzen dute, norabide berbera, alderantzizko norantza eta ekintza lerro berbera duten indarrak direlako. Indar hauek lor dezaketen gauza bakarra espira deformatzea izango litzateke, baldin eta honek behar heineko gogortasuna izango ez balu.

F₄ eta F₂ indarrak, aldiz, ez dute ekintza lerro berbera (Ï•=0 ez bada behintzat); a·sinÏ• distantziak banatzen ditu eta, beraz, indar bikote horien momentua hauxe izango da.

Kontutan hartuta

Espiraren gainazalaren azalera S=a·b bada:

Eta adierazpen hau era bektorialean ipiniz:

Indarren momentuaren ezaugarriak honakoak izango dira:

• MODULUA: 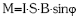izango da. Indar bikotearen momentua ezeztatu egiten d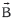a eta 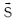bektoreak lerrokatuta daudenean. Hori espira eremu magnetikoaren indar lerroekiko perpendikularra jartzen denean gertatzen da. Momentua, aldiz, maximoa izango da espiraren planoa eremu lerroekiko paraleloa denean.
• NORABIDEA: espiraren gainazal bektoreak eta eremu magnetikoak osatzen duten planoarekiko elkarzuta izango da.
• NORANTZA: sakakortxoaren erregelarena.

magnitude bektorialari espira lau baten MOMENTU MAGNETIKOA deitzen zaio. Momentu magnetikoak gainazal bektoreak duen norabide eta norantza berbera dauka. Hortaz, beti izango da espiraren gainazalarekiko perpendikularra.

Momentu magnetikoaren definizioan oinarrituz, espira baten gainean eremu magnetiko uniforme batek eragiten duen momentua zera izango da:

Zirkuitua gainezarritako N espira lauek osatzen badute, aurreko adierazpena honela geratuko da:

Azpian daukazue funtzionamenduaren oinarria adierazten duen bideo bat:

How To Build A Simple Electric Motor, Plus How It Works. – Celebrity bloopers here

Kontutan hartzekoak

A) GOGORATU! gainazal bektorea espiraren planoarekiko elkarzuta den bektore bat da, non bektore honen moduluak espiraren azalera ematen digu.

B) Espira zirkular baten kasurako emaitza berdinak lortzen dira, baina azken kasu honetan, kalkuluan zailtasuna areagotu egiten da.

Proposatutako ariketak

15.- Espira lau baten momentu magnetikoa  A·m² adierazpenaren bitartez emana dator eta  T-ko indukzio magnetikoa duen eremu batean murgildurik aurkitzen da. Kalkulatu:

1. Espiraren azaleraren balioa, bertatik 2 A-tako korronte elektriko bat pasatzen bada.
2. Espiraren gainean eragiten duen indar pareak sortzen duen momentua.

16.- 1000 espirako bobina bat 0,5 T-tako eremu magnetiko uniforme batean murgiltzen da. Espiren erradioa 2,5 cm-ko erradioa badute eta bertatik 1,4 A-tako korronte bat zirkulatzen badu, aurkitu:

1. Bobinaren momentu magnetikoa
2. Bobinaren gainean agertzen den indar pareak sortutako momentua, eremu magnetikoak eta momentu magnetikoak 30ï‚°-ko angelua eratzen dutenean.
3. Momentu horren balio maximoa