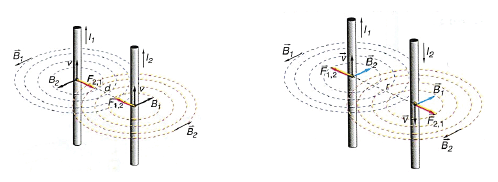
Bi korronte paraleloren eta mugagaberen arteko elkarrekintza aztertuko dugu jarraian, kontuan hartuta d distantziara daudela, I₁ eta I₂ korronteak igarotzen direla eta korronte biak norantza berean higitzen direla.

I₁-ek I₂ eroalearen puntu batean sortutako eremu magnetikoaren indukzioa B1 izango da, berau Biot-Savarten erregelan oinarrituta lor daitekeelarik:

Bestalde, eremu magnetiko honek hari eroale zuzen baten gainean eragiten duenez eta bertatik korronte bat pasatzen denez, hariaren gainean indar bat eragingo du; Laplacen lehenengo legean oinarrituz:

Beraz:

Hau da:

Biderkadura bektorialaren definizioan oinarrituz, lehenengo hariak bigarrenari eragiten dion indarra bi hariek osatzen duten planoan egongo da eta biekiko perpendikularra izango da.

Era beretsuan, deduzitu daiteke bigarren hariak lehenengoari eragingo dion indarra. Akzio-erreakzio printzipioan oinarriturik:

F_1,2=-F_2,1

Kontsideratutako harietatik pasatzen diren korronteen norantzak berdinak izanik, bi hariak elkar erakarri egiten direla erraz ikus daiteke. Aurkakoa gertatuko da baldin eta harietatik eroaten diren korronteek aurkako norantza badute.

Kontutan hartzekoak

A) Metro batera bananduta eta 1 A-tako korronteak igarotzen dituen bi eroale lerrozuzen eta mugagabetako 1 m-ko luzerako segmentuen arteko erakarpen indarra ondokoa da:

Azken adierazpen honi esker, AMPEREA modu esperimentalean definitzeko aukera dugu:

Amperea, zuzenak, paraleloak eta mugagabeak diren eta metro bateko distantzian dauden bi eroaleetatik norantza berean igarotzen den korronte intentsitatea da; hori gertatzen denean, eroaleek elkarri eragingo diote eroale metro bakoitzeko 2·10^-7 N-eko indarrarekin.

Proposatutako ariketak

17.- X, Y eta Z orriaren planoarekiko perpendikular diren hiru eroale dira eta, gainera, elkarren distantziakideak dira. X eta Z korronteak orrirantz sartzen dira; Z korrontea, ordea, irten egiten da.

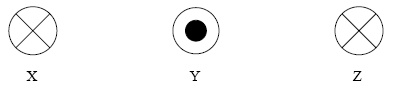
Y eroaleari eragiten dion indar elektromagnetikoa honelakoa da:

1. Nulua
2. Hiru eroaleak lotzen dituen lerroarekiko perpendikularra.
3. Y-tik Z-rako norabidea eta norantza edukiko du.
4. Y-tik X-rako norabidea eta norantza edukiko du.
5. Norantza hiru korronteen intentsitatearen araberakoa izango da.

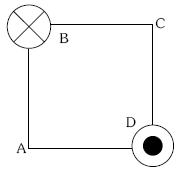
18.- 3 A eta 4 A-tako korronteak zeharkatzen dituzten bi hari metaliko luze eta paralelo, plano elkarzutean kokatuta dagoen 2 m-ko aldea duen karratu baten B eta D ertzetatik pasatzen dira, irudian adierazten den bezala. Korronteen norantzak kontutan harturik, adierazi eskema batean eta kalkulatu, horietako bakoitzaren gainean agertzen den elkarrekintza magnetikoaren balioa eta A erpinean agertzen den eremu magnetiko ordezkaria.

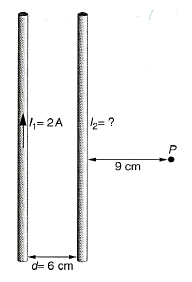19.- 6 cm-ko distantziara dauden bi hari zuzen, paralelo eta luzeetatik bi korronte pasatzen dira: batek I1=2 A-tako intentsitatea dauka eta bestea I2-koa, I1 korrontearen norantza adierazten dena izanik. Kalkulatu ezazu I2-ren balioa eta norantza P puntuko eremu magnetikoa nulua izan dadin. Kalkulatu eroale biek elkarri egiten dioten elkarrekintza indarra luzera unitateko.

DATUA: 4π·10^-7 m·kg·C^-2