Azpiko irudian ikus daitekeen bezala trena trenbide zirkularretik higitzen ari da. Bere abiadura, uneoro ibilbidearekiko tangentea mantendu behar dena, norabidez aldatzen doa azelerazio normal baten menpe baitago.
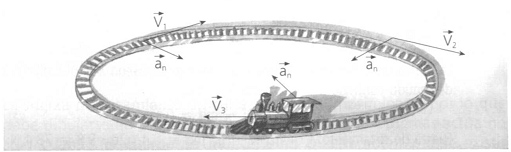
Ibilbide zirkularrean, abiaduraren norabidearen aldaketa denboraren baitan modu konstantean ematen denez, azelerazio normal edo zentripetua konstantea izango da moduloz eta jhonen zentrurantz zuzenduta egongo da. Bere modulua ondorengo erlazioaren bitartez adierazi daiteke:
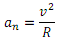
non v trenaren abiadura lineala den eta R trenbidearen zirkunferentziaren erradioa.
Newtonen bigarren printzipioaren arabera, azelerazio duen edozein gorputz baten gainean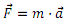 
indar batek eragin beharko du azelerazio honen norabide eta norazko berean. Kasu honetan indar zentripetua deitzen dugu, zirkunferentziaren zentrorantz zuzenduta egonik.
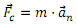
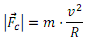
Jarri dugun adibidean, indar zentripetua trenbideak eragiten du trenaren gurpilen gainean, euren norabidea aldarazten duelarik. Ezinezkoa izango litzateke trenak ibilbide zirkularra deskribatzea kartulina batean marraztutako trenbide baten gainetik desplazatuko balitz, izan ere, zirkunferentzia deskribatzeko beharrezkoa den indar zentripeturik ez litzateke agertuko.
Gorputz bati ezartzen zaizkion indarren erresultantea indar zentripetua denean, gorputz hori higidura zirkular uniformez higitzen da.
Horixe gertatzen da, adibidez, soka bati lotutako gorputz bat bira bertikalak deskribatzea behartzen dugunean edota kotxe batek errepideko kurba bat hartzen duenean. Kasu hauetan guztietan, indar zentripetu baten presentzia egongo da; lehenengo kasuan sokaren tentsioa izango da eta bigarrenean errepidearen marruskadura indarra.
Aurreko guztia horrela da baldin eta behatzailea inertziala bada, alegia, higidura zirkularra deskribatzen ari den gorputzatik kanpo dagoen behatzaile batentzat. Batzuetan, ordea, behatzaileak berak deskribatzen du higidura zirkularra. Behatzailea sistema ez-inertzial batean aurkitzen denean, aurreko atalean aipatu dugun bezala, bere gainean indar ez-inertzial batek eragiten du. Indar hau, zentripetua ez bezala, kanporantz agertzen da eta derriogorrezkoa izango dugu aintzat hartzea Newton legeak betetzea nahi badugu. Kurbatik irtetera eragiten digun indar ez-inertziala honi indar zentrifugoa deitzen diogu eta indar zentripetuaren balioarekin bat dator. Beraz, kurbatik irtetea ez badugu nahi kanporantz agertzen den indar honen aurka modulu bereko beste bat agertuko behar da. Horrela bakarrik lortuko dugu gorputzak bere higidura zirkularra mantentzea.
Ebaztutako ariketa
10.-100 kg-ko kotxe batek 20 m-ko erradioa duen kurba bat hartzen du . Marruskadura koefizientea 0,2 bada, aurkitu:
- Lurra laua izango balitz, kotxeak eramango lukeen abiadura maximoa lateralki ez irristatzeko.
- 15º-ko peraltea egongo balitz, zein izango litzateke abiadura hori?
Proposatutako ariketak
11.-Pista baten kurbak 20º-ko peraltea du eta bere erradioa 70 metrkoa da. μ=0 bada, kalkulatu higikari batek, kurbatik atera gabe, eraman dezakeen abiadurarik handiena. Kurba horizontala izango balitz eta abiadura hau eramanez, zein izan beharko litzateke marruskadura koefizientearen balioa higikaria kurbatik ez ateratzeko?
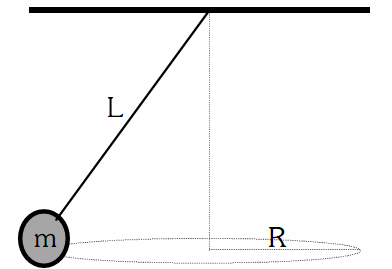
12.-Grafikoko m masako goputzak 70 cm-ko erradioko zirkunferentzi horizontaletan bira egiten du, sapaiatik 80 cm-ko luzerako soka batez loturik dagoelarik. Bilatu:
- Gorputzak sufritzen duen indar zentripetua
- Sokaren tentsioa.
13.-Bila ezazu “tubo de la muerte†deritzon tresnan lan egiten duen motoristaren abiadura minimoa eror ez dadin. Pareta eta gurpilaren arteko marruskadura koefizientea ï da.