Newtonen ikerketek astronomiaren alorrean Grabitazio Unibertsalaren Legea postulatzea eraman zuten. Honen bitartez, Lurraren (edo beste edozein planetaren) gainean gorputzen erorketa edota planeten higidura nola ematen den esplikatzen zuen. Hala ere, ezagutza zientifikoarentzat hain garrantzitsuak ziren ekarpen hauek arazo bat suposatzen zuten: nola eragiten du grabitatearen indarrak elkar ukitzen ez diren gorputzen artean?.

Behatutako edota esperimentalki aztertutako gertaera hauei esplikazio bat emateko, ezagutza zientifikoan eragin izugarria izan zuen kontzeptu berri baten beharra ikusi zen: EREMU kontzeptua hain zuzen ere. Eremu kontzeptuaren bitartez distantziara agertzen diren elkarrekintzak esplikatzen ziren.

Horrela, eremu grabitatorioa gorputz materialen (hau da, masadun gorputzen) arteko elkarrekintzaren arduraduna izango litzateke. Baina nola definitu eremu grabitatorioa?.

Imajina dezagun erabat hutsik dagoen espazio eskualde bat. Bertan m₁ masako gorputz material bat ipintzen dugu. Gorputz hori bakarrik egotean bere gainean ez litzateke inongo indarrik agertuko. Gauza berbera gertatuko litzateke honen ordez m₂ masako beste gorputz bat ipiniko bagenu. Baina, lehenengo masa puntu finko batean ipiniko bagenu eta ondoren bere inguruko punturen batean bigarrena, honen gainean indar batek eragiten duela ikusten da.

Beraz, masa batek bere inguruan sortzen duen grabitazio eremua aipatutako masaren eraginpean dagoen eremuan objektu bat jartzen dugunean nabaritzen dugu, izan ere, eraginpeko eremu horretan objektua jartzean indarra jasango du, bere balioa grabitazio unibertsalaren legearen araberakoa delarik.

Lurreko eremu grabitatorioa Lurrari dagokion grabitazio unibertsalaren kasu berezia da.

Lurreko eremu grabitatorioa espazioko eskualdea da non bertako puntu bakoitzean kokatuta dagoen edozein masa materialaren gainean Lurraren erakarpen akzioa guztiz definituta dagoen.

Eremu grabitatorioan kokatzen den gorputzak nabaritzen duen indarraren ezaugarriak honako hauek dira:

• MODULUA: Grabitazio Unibertsalaren Legeak adierazten duena.

non m gorputzaren masa, M_L Lurraren masa eta R gorputzaren zentrotik Lurraren zentroraino dagoen distantzia diren.

• NORABIDEA: gorputzen zentroak lotzen dituen zuzenarena. Beraz, eremu grabitatorioa eremu ZENTRALA da.

• NORANTZA: aurreko atalean ikusi dugun bezala eta aurkako norantza dute eta, ondorioz, indar hau beti erakarpenezkoa da.

Beraz, grabitazio eremua LOTURA eremua da.

EREMU GRABITATORIOAREN INTENTSITATEA

M masa batek bere inguruan sortzen duen eremu grabitatorioan m1 masa bat ipintzen badugu R distantziara, bere gainean F₁ indar bat agertuko da. Distantzia berberera m₂ beste masa bat ipintzen badugu, bere gainean F₂ beste indar ezberdin bat agertuko da. Beraz, ikusten da distantzia jakin batean gorputz baten gainean agertzen den indarra puntu horretan ipintzen den gorputzaren masaren menpe dagoela.

Eremu grabitatorioaren intentsitatea (g) espazioko puntu batean, puntu horretan kokatutako masa unitatearen gainean agertzen den indarra da.

Honela, M masa puntualak P puntuan sortzen duen eremu grabitatorioaren intentsitatea kalkulatzeko, puntu horretan m masa bat ipintzen dugu eta bere gainean agertzen den indarra kalkulatuz, bien arteko erlazioa aurkituko dugu:

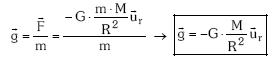
Eremu grabitatorioaren intentsitatearen ezaugarriak hauek dira:

• MODULUA: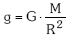. Ikusten denez bat dator 1 kg-ko masak R distantziara nabaritzen duen indarraren balioarekin.

• NORABIDEA: masaren zentroa eta kontsideratutako puntua lotzen duen zuzenarena.

• NORANTZA: indar grabitatorioarenaren berdina, hau da, puntutik masara zuzendua.

EREMU GRABITATORIOAREN GAINEZARMEN PRINTZIPIOA

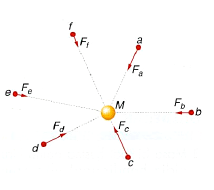
Demagun grabitazio eremua M₁, M₂, M₃, …, Mn masadun gorputzek osatzen dutela (esaterako, gure Eguzki-sisteman gertatzen den bezala). Puntu jakin batean gorputz horiek guztiek sortzen duten grabitazio eremuaren intentsitatea kalkulatzeko GAINEZARMEN PRINTZIPIOA erabili dezakegu: izan ere, gorputz bakoitzak intentsitatea eragingo du puntu horretan eta intentsitate horien batuketa bektoriala eginez lortuko dugu grabitazio eremuaren intentsitate osoa. Beraz:

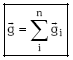
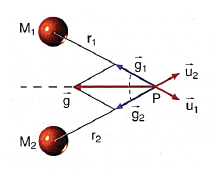M₁ eta M₂ masadun bi objektuen kasuan (masak puntualak direla jota) sortutako grabitazio eremuaren intentsitatea honakoa da:

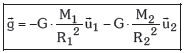
EREMU GRABITATORIOAREN IRUDIKAPEN GRAFIKOA

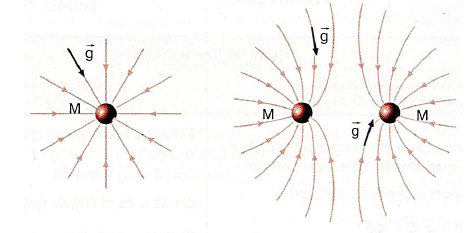
Eremu grabitatorioa bezalako indar eremu bat bere INDAR LERROEN bitartez adierazi daiteke. Indar lerroak irudikatzeko zera izan behar dugu kontutan: puntu bakoitzean eremu grabitatorioaren intentsitatea lerro hauekiko ukitzailea izan behar da eta bere norantza lerro hauen berdina izan behar da.

Bestalde, eremu lerroen dentsitatea (lerroekiko perpendikularki kokatutako azalera unitate bakoitza zeharkatzen duen lerro kopurua) eremu grabitatorioaren intentsitatearen moduluarekiko proportzionala izan behar da. Honen arabera eremu grabitatorioak intentsitate handiagoa du eremu lerroak ondo-ondoan aurkitzen diren eskualdeetan.

Kontutan hartzekoak

1) Distantziara agertzen diren elkarrekintzen azterketa ez dugu bakarrik gai honetan egingo.

Hurrengo bi gaietan INDAR ELEKTRIKOA eta INDAR MAGNETIKOAK ikusiko ditugu. Indar hauek ere, distantziara ematen diren elkarrekintzak dira, eta ondorioz, beraien ezaugarriak azaltzeko EREMU kontzeptura jo beharko dugu ere.

2) Grabitazioa Einsteinen Arabera: Albert Einstein fisikari alemaniarrak, masa batek, berau inguratzen duen espazio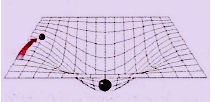a nola perturbatzen duen azaltzeko, ondorengo eredua proposatu zuen.

Oihal elastiko baten erdian bola astun bat kokatzen badugu, bere pisuaren ondorioz oihala deformatzen du erdiko puntuan. Ondoren, beste bola arinago bat lehenengoarekiko gertu kokatzen badugu, ohartuko gara bolatxoaren ibilbidea pixkanaka desbideratzen dela bola astunerantz inguratuz.

Eguzkiak bere inguruan sortzen duen eremu grabitatorioaren ondorioz, Lurraren mugimendua Eguzkiaren inguruan era beretsuan gertatzen dela suposa dezakegu.

SI-ko unitateak

Magnitudea	Ikurra	Unitatea
Indarra	F	Newton (N)
Intentsitatea	g	N·kg-1

Ebaztutako ariketa

5.-1 m-ko aldea duen triangelu aldekide baten hiru erpinetan 1, 2 eta 3 kg-ko hiru masa finko ipintzen dira, hurrenez hurren. Aurkitu ezazu triangeluaren erdian kokatutako 2 kg-ko masa baten gainean agertzen den indar grabitatorioa. (Ebazpena – pdf, 40 Kb)

Proposatutako ariketak

6.- Irudian agertzen den sisteman, kalkulatu P puntuak jasaten duen eremuaren intentsitatea, masa bakoitza 3,2 kg-koa bada.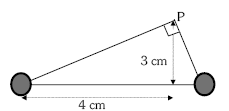

7.- Lurraren gainazalean gorputz baten pisua P da. Non egon behar da bere pisua erdia izateko?

8.- Har dezagun Lurra esfera homogeneo bat bezala non eremu grabitatorioaren intentsitatea bere gainazalean 9,8 rn/s² da. Izugarrizko leherketa nuklear baten ondorioz kanpo aldean dagoen planetaren masa totalaren erdia desagertzen da. Zein izango da orduan Lurrak bere gainazalean izango duen grabitate berria?