Gaur egun, jadanik, inor ez da harritzen Ilargi berriak bailitzan, Lurraren inguruan orbita eliptikoetan (zirkularrak kontsidera daitezkeenak) biratzen duten satelite artifizialen agerpenaz. Satelite hauek, batzuek helburu baketsuak dituztenak (ikerketa, komunikazioak,…) eta beste batzuek belikoak, 30.000 km/h-ko inguruko abiadurarekin biratzen dute Lurraren inguruan.
Baina, sateliteak orbitan ipintzea ez da izan azken urte hauetako arazoa bakarrik. Jadanik, Newton-ek ere proposatu zuen nola izango litzateke posible kanoi batetik jaurtitako jaurtigai batek Lurrari bira oso bat ematea.
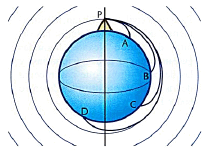 Newton-ek zera proposatzen zuen: mendi handi baten P altuera batean kanoi bat kokatuko bagenu, jaurtigai bat abiadura horizontalarekin jaurtitzerakoan, bere ibilbidea zuzena izan beharko litzateke indar grabitatorioak ez balu bere ibilbidea kurbatuko jaurtigaia Lurrera erori eraziz.
Newton-ek zera proposatzen zuen: mendi handi baten P altuera batean kanoi bat kokatuko bagenu, jaurtigai bat abiadura horizontalarekin jaurtitzerakoan, bere ibilbidea zuzena izan beharko litzateke indar grabitatorioak ez balu bere ibilbidea kurbatuko jaurtigaia Lurrera erori eraziz.
Jaurtigaiari abiadura handiagoa emanez, A puntuan baina urrutiago eroriko litzateke eta horrela abiadura handituz, kurbadura txikiagoa izango litzateke, irispidea handituz. Beraz, logikoa ematen du pentsatzea abiadura nahikoa emanez gero jaurtigaia P puntura bueltatuko litzatekeela lurrera erori gabe. Hau da, grabitatearen indarrak bakarrik bere ibilbidea kurbatuko luke. Azalpen honen bitartez, Newton-ek planeten higidura Eguzkiaren inguruan nola ematen den esplikatu nahi zuen eta era berean Lurraren inguruan satelite artifizialak ipintzeko posibilitatea planteatu zuen.
Praktikan garbi dago, satelite horiek behar duten abiadura lortzeko kanoirik ezin dela eraiki. Bere ordez, koheteak erabili daitezke satelite horiek altuera egokian ipintzeko.
IHES ABIADURA
Zientziak, planetarteko bidaien arazoa serioski mahaigaineratu zuenean, azaldu behar izan zuen lehenengoetariko arazoa IHES-ABIADURA deitutakoaren kalkuluarena izan zen, edo baita, kohete baten jaurtiketan, Lurraren erakarpenetik aska dadin, beharrezkoa den abiadura minimoa.
Lurraren gainazaletik botatzen den jaurtigai batek grabitate ekintzari “ihes†egin diezaion eta planetara itzuli ez dadin nahi bada, jaurtigai horren masa Lurraren gainazaletik “infinituraino†eramateko behar den lanaren baliokidea den energia eman beharko zaio hasieran.
Infinitura heltzerakoan EP=0 denez eta Ez=0 ere bai, bertan bere energia mekaniko osoa nulua izango da: Em(∞)=0 Eremu grabitatorioa kontserbakorra denez, Lurraren gainazalean untzi espazialaren energia mekanikoa ere nulua izan beharko da. Beraz:

Eta ondorioz:
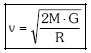
Hauxe da, hain zuzen, untzia bidaltzeko behar dugun gutxieneko abiadura.
SATELITE BATEN ORBITA ALDAKETA
Satelite bat orbitaz aldatu erazi nahi denean, energia kantitate bat irabazi edo galdu erazi behar zaio, baldin eta orbita berria aurrekoarena baina altuera handiagora edo txikiagora baldin badago.
Energia balio hori kalkulatzeko, nahikoa da energiaren kontserbazio printzipioa aplikatzea bi orbitetan satelitearen energia mekanikoa berdina izan behar baita.
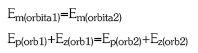
PLANETA EDO SATELITEEN ABIADURA ORBITALA
Planeta baten edo satelite baten higidura grabitazio legearen menpe dauden elkarrekintza grabitatorioen ondorioa da. Gorputz batek beste batekin elkarrekintza duenean, gorputz biek jasaten dute eragina. Newton-en hirugarren legearen arabera, gorputz biek jasaten dute intentsitate eta norabide berdineko baina aurkako norantzako indarra.
Dena dela, aipatutako elkarrekintzak eragin desberdinak izan ditzake bi gorputz horiengan, eragin hori masaren araberakoa bait da.
Orain egingo ditugun kalkuluetan bi gorputzen artean gertatzen den elkarrekintzan gorputz baten masa bestearena baino askoz handiagoa dela joko dugu. Hori kontutan hartuta, masa handiagoa duen gorputza geldirik egongo dela eta masa txikiagokoa haren inguruan biraka ibiliko dela jo dezakegu.
Satelite bat Lurraren inguruan biraka dabilenean (edota planeta bat Eguzkiaren inguruan), bere gainean agertzen den indar bakarra erakarpen grabitatorioarena da. Atal honen hasieran ikusi dugun hezala, indar honek satelitearen abiaduraren norabidearen aldaketa behartzen du. Beraz, indar zentripetu bat izango da. Newton-en bigarren legea aplikatuz:
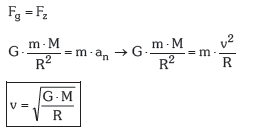
Sateliteak orbita oso bat betetzeko behar duen denborari BIRAKETA PERIODOA deritzo edota ORBITA PERIODOA. Periodoa abiadura orbitalarekin erlaziona daiteke:
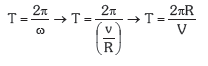
Eta ondorioz:
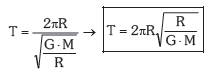
Ebaztutako ariketa
9.- Lurra RL=6370 km erradioa duen esfera homogeneoa dela suposatuz:
- Lurraren gainazaletik 630 km-tara dagoen P puntu batean grabitatearen azelerazioaren balioa aurkitu.
- P puntu batean masa bat, hasierako abiadurarik gabe , askatuko bagenu, zein abiadurarekin helduko litzateke Lurraren gainazalera?. (Ebazpena – pdf, 37 kb)
DATUAK: G=6,67·10-11 N·m-2·kg2; ML=5,98·1024 kg
Proposatutako ariketak
10.- Orbita zirkular ekuatorialean jarri nahi da 50 kg-ko satelite artifizial bat, bere erradioa Lurraren erradioaren bikoitza delarik.
Kalkula bitez:
- Sateliteari eman beharko zaion energia eta bere abiadura orbitala.
- Behin orbita horretan egonez gero, sateliteari gehitu beharko geniokeen energia Lurren eremu grabitatorioaren erakarpenetik ihes egin dezan.
DATUAK: G=6,67·10-11 N·m-2·kg2; ML=5,98·1024 kg; RL=6,37·106 m
11.- Suziri baten bidez, gorputz bat itsasmailatik 500 km-tako altuerara eraman da.
- Altuera horretan, zein da Lurreko eremu grabitatorioaren intentsitatea?
- Zein abiaduraz jaurtiki beharko da gorputz hau, Lurraren erradioarekiko norabide perpendikular batean, orbita zirkular bat deskriba dezan?
- Zein izango litzateke gorputzaren biraketa periodoa Lurraren inguruan?.
- Gorputzaren masa 100 kg-takoa bada, zein izango da bere energia mekanikoa?
DATUAK: G=6,67·10-11 N·m-2·kg2; ML=5,98·1024 kg; RL=6,37·106 m
12.- Lurraren eta Ilargiaren erradioak, 6378 km eta 1738 km-takoak dira. Lurraren eta Ilargiaren masen arteko erlazioa 81,3 da. Lor bitez:
- Ilargiaren gainazalean dagoen grabitatearen azelerazioa, Lurraren gainazalean dagoena 9,8 m·s-2-koa bada
- Ilargiaren gainazalean dagoen gorputz bati eman behar zaion ihes abiadura, hau da, Ilargiaren grabitatearen erakarpenetik ihes egiteko behar duen abiadura.
13.- 1000 km-ko erradio duen planeta batean, grabitatearen azelerazioa 2 m·s-2 da. Kalkulatu:
- Planetaren gainazalean aurkitzen den 50 kg-ko objektu baten energia potentzial grabitatorioa.
- Planetaren ihes abiaduraren balioa.
- Planetaren masa.
DATUAK: G=6,67·10-11 N·m-2·kg2
![]() Webgune Interesgarriak
Webgune Interesgarriak
- Sateliteen higidura nola ematen den ulertzeko hona hemen CloudSat eta Calipso sateliteen inguruko artikulu interesgarria, batak atmosfera ikertuko du eta besteak klima aldaketarekin lotura izango duten fenomenoak. Bi satelite hauek lurrari bira emango diote A-Train izenko satelite trenari lotuta. Artikuluan ere, NASAK sorturiko simulazio sorta bat ere beha daiteke satelite hauen funtzionamendua ulertzeko.
Hor norbait baldin badago, kaixo!
11. ariketari dagokionean, zalantza bat sortu zait honen b atalari erantzuteko orduan:
behin orbitan egonez gero, sateliteari eremu grabitatorioaren erakarpen indarretik ihes egiteko zein energia eman beharko geniokeen galdetzen da.
2 modu bururatu zaizkit erantzuteko, baina kuestioa da ez dutela erantzun berbera ematen:
1) eremu grabitatorioaren erakarpen indarretik ihes egiteko, gorputza puntu horretatik infinitora eraman beharko dugu, infinitoan lortuko baitu erakarpen indarraren eraginik ez izatea. (Fg=0) Beraz, lan bat burutu beharko dugu gorputza puntu horretatik infinitora eramateko, hain zuzen ere, eman beharreko energia hori (eskatzen digutena). Definizioz, puntuko energia potentzialaren balioak emango digu emaitza.
2) Eremu grabitatorioaren erakarpen indarretik ihes egitea nahi badugu, nahikoa da Fg
Link | 15 martxoa, 2006 at 19:37
Fz baino txikiagoa izatea: gorputzak erakarpen indarrari “ihes egingo dio”: beraz, gorputzaren abiadura handitu beharko dugu bere Ez handituz, Fz handiagoa izan dadin. Beraz, Ez handiago bat litzateke emaitza
Zein dago zuzen (baten bat zuzen baldin badago)???
Link | 15 martxoa, 2006 at 19:41
Beste galdera bat, 12. ariketako d atalari erantzuteko orduan:
Em kalkulatzeko, Ep eta Ez batu beharko ditugu. Ordea, Ep negatibo bezala hartuko al dugu??? Kasu horretan Em negatiboa litzateke. Posible al da hori??
Link | 15 martxoa, 2006 at 19:43
1) Ez nahastu orbita aldaketa gertatzeko gorputzak irabazi behar duen energia zinetikoa eta, orbitan ari denean, sateeliteak duen energia zinetikoa. Kontuz!
2) Energia mekanikoa negatiboa izatea gorputza eremuari lotuta dagoela adierazten du. Bere energia mekanikoa positiboa izango balitz eremutik aske dagoen gorputz batetaz arituko ginateke.
Link | 15 martxoa, 2006 at 20:15
Kaixo denoi!
Ariketak egiten ari naizela, dudatxo batekin egin dut tupust. 13. ariketako b atalean Grabitazio unibertsalaren konstantearen (G) beharrean aurkitzen naiz ilargiko gorputzaren ihes abiadura kalkulatzerakoan. Bere balioa eman ez diguzunez dudatan geratu naiz. Zer egingo dut, G-ren baitan utzi, bere balioa ordezkatu, edo, agian, beste bide batetik joanez ebaztu behar da ariket(e)a?
Edonoren erantzunaren zain… Ibai.
AIO!
Link | 16 martxoa, 2006 at 20:09
Aupa Ibai.
Ez bat eta ez bestea. Ariketaren bigarren atalean, eman ezazu ilargian duen ihes abiaduraren balioa lurreko ihes abiaduraren baitan (azken honen balioa ezezaguna izan arren). Hori da guztia
Eman gogor!
Link | 16 martxoa, 2006 at 21:18