Aurreko atalean, saiakuntza bidez lortutako emaitzak aztertu ondoren, galdera batekin egin dugu topo: ba al da aipatutako saiakuntzak biltzen dituen lege fisikorik?.

Saiakuntza hauetatik hiru ondorio nagusi atera daitezke:

• Zirkuitu itxi batez osatutako sistema bat perturbatzen denean (iman edo bobina baten mugimendu erlatiboaren ondorioz edota honi akoplatutako bigarren zirkuitu baten intentsitatea aldatuz), bertan korronte elektriko bat induzitzen da.
• Sortzen den perturbazioa aztertzen ari garen zirkuituaren gainazala zeharkatzen duten eremu lerro kopuruaren araberakoa da. Hau da, fluxu aldaketaren araberakoa.
• Induzitutako korrontea are eta intentsuagoa da baldin eta sortutako fluxu aldaketa are eta azkarrago ematen bada. Hau da, fluxu aldaketak irauten duen denbora tartearen araberakoa da ere.

Beraz, zera ondorioztatu daiteke:

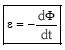
Zirkuitu bat zeharkatzen duen fluxu magnetikoaren aldaketak indar elektroeragile (iee) induzitu bat sortzen du fluxuaren aldaketa ematen den azkartasunarekiko zuzenki proportzionala delarik

Esperimentu askotan ezin da jakin zein den fluxuaren aldaketaren eta denboraren arteko erlazioa. Horrelakoetan ezin dugu denbora une bakoitzean fluxuaren aldaketa nola eman den aztertu. Baina posiblea da denbora tarte batean (Δt) gertatu den batezbesteko fluxu aldaketa (ΔΦ) neurtzea. Kasu honetan, nahiz eta aldiuneko iee ezin kalkulatu, posiblea da denbora tarte batean gertatu den batezbesteko indar elektroeragilearen balioa lortzea.

Azkenik, induzitutako korrontea espira batean sortu beharrean N espiratako bobina batean induzitzen bada, indar elektroeragilearen balioa hurrengo adierazpenak emango digu:

Lenz-en Legea

Orain arte fluxu aldaketaren ondorioz agertzen den korrontearen intentsitatearen balioaz jardun gara baina ez dugu aipatu zein norantzatan agertzen den induzitutako korronte hau.

Induzitutako korrontearen norantza zehazteko erregela Lenz-ek eman zuen 1834ean eta LENZ-EN ERREGELA bezala kontsideratzen da: Induzitutako korrontearen norantza fluxu induktorearen aldaketak eragozteko norantza hartuko du. Hau da, induzitutako korrontea berau sortarazten duen kausari oposatzen zaio.

Faraday-ren legearen adierazpenaren zeinu “-“-ak azaltzen du, hain zuzen ere, Lenz-en legea: induzitutako korrontea fluxuaren aldakuntza positibo batentzat izan bada, korrontearen norantza fluxuaren aldakuntza txikitzearen aldekoa izango da eta alderantziz. Horrela, erraz zehaztu daiteke induzitutako korrontearen norantza.

Kontutan hartzekoak

---

A) Faraday-Henryren legea kuantifikatu nahi badugu, korronte induzitua karakterizatu behar dugu. Horretarako magnitude fisiko bat behar dugu; magnitude hori korronte induzituaren intentsitatea edo indar elektroeragile induzitua izan daiteke.

Korrontearen intentsitatea ez da egokia, espira egiteko erabilitako materialaren erresistentziaren araberakoa delako. Hortaz, korronte induzitua karakterizatzeko espira zeharkatzen duen fluxu magnetikoa aldatzean espiran agertzen den indar elektroeragile induzitua erabiltzea komeni da.

B) Lenzen legea energiaren kontserbazio printzipioaren ondorioa da. Induzitutako korrontearen norantza bera sortarazi duen kausaren aldekoa izango balitz, energia mugagabe bat izango genuke hutsetik abiatuta. Baina hau ez da posiblea.

Ariketa Ebaztuak

---

20.- 0,005 m-ko erradioa duen eta 500 espiraz osatua dagoen hari eroalez eratutako karrete bat, 0,1 T-tako eremu uniforme batean kokatzen da, berau zeharkatzen duen fluxua maximoa den orientazioarekin.

1. Aurkitu ezazu karretean induzituriko i.e.e., 0,02 s-tako denbora tartean eremua bikoizten bada.
2. Aurkitu ezazu karretean induzituriko i.e.e., karreteak 180º biratzen baditu 0,02 s-tan eremuarekiko elkarzuta eta karretearen zentrotik pasatzen den ardatz batekiko. (Ebazpena – pdf 33 kb)

Ariketa Proposatuak

---

21.- 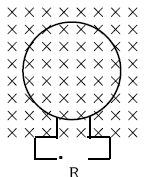1,5 Ω-ko erresistentzia duen espira bat 3000 Teslako eremu magnetiko batetan perpendikularki kokatuta dago irudian ikusten den bezala. Espiraren azalera aldakorra da, denborarekiko honela aldatuz:

(azalera m²-tan eta denbora segundotan). Kalkulatu:

1. t=5 s eta t=15 s denean zirkuituaren intentsitatea.
2. Irudikatu zein norantzatan mugituko den korrontea bi instante hauetan.

22.- Bobina batek 0,2 T-tako eremu magnetiko uniforme batean biraka dabil 20 rad/s-ko abiaduraz. Aurkitu ezazu induzituriko i.e.e.

DATUAK: Bobinaren erradioa: R=60 cm
                  Espira kopurua: N=100

23.- 10 cm-ko aldea duen espira karratu bat bere zentrutik pasatzen den ardatz bertikal baten inguruan biraka dabil, 0,5 T-tako eremu magnetiko uniforme eta horizontal batean. Espira eremuarekiko perpendikularki kokatuta badago, zein izan behar da bere abiadura angeluarra, bertan 5 v-tako i.e.e. maximoa duen korronte bat induzitzeko?.

24.- Espira eroale bat zeharkatzen duen fluxu magnetikoa Φ=(t²-4t)·10^-1 T·m² formulak emana dator, t segundotan.

1. Aurkitu ezazu i.e.e. induzitua denboraren funtzioan
2. Adieraz ezazu grafikoki fluxuaren eta i.e.e.-aren aldaketa denborarekiko
3. Zeintzuk aldiuneetan bihurtzen da zero fluxua?. Zein da i.e.e.-aren balioa aldiune horietan

25.- 2,5 A-ko korronte zuzen batek 500 espira dituen harila elikatzen du eta bertan 3,6·10^-4 wb-eko fluxu magnetikoa eragiten du. Ondoriozta ezazu harilaren autoindukzio koefizientea, korrontea eten ondoren 0,06 segundora fluxua anulatu egiten dela jakinik.