Higikari batek bere ibilbidearen gainean duen posizioa, A, zehazteko, ondorengoa egin dezakegu:
- Erreferentzi modura ibilbideko O puntu bat hartu.
- O eta A-ren arteko ibilbidea irudikatu.
- O jatorria eta A puntua banatzen dituen distantzia, ∆s.
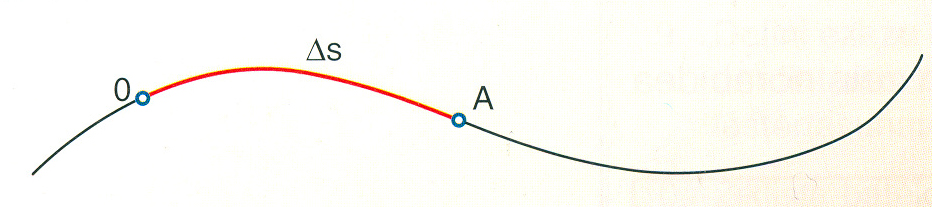
Ibilbideko edozein punturi lotu diezaiokegu ibilbidearekiko ukitzailea den ardatz batek eta ibilbidearekiko perpendikular den beste ardatz batek eraturiko erreferentzi sistema. Erreferentzi sistema hori, beraz, ibilbidearekiko intrintsekoa da.
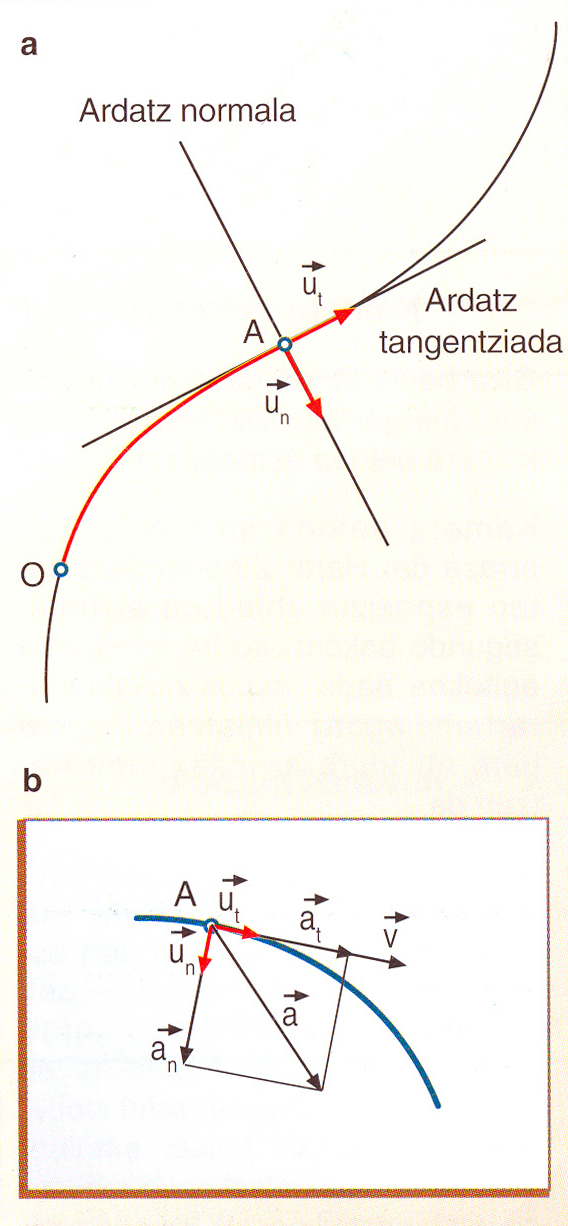
Azter ditzagun zeintzuk diren bi ardatz hauen ezaugarri nagusiak:
- Ardatz tangentziala: OA arkua osatzen duten edozein puntutan, ardatz hau ibilbidearekiko ukitzailea izango da beti. Bat etorriko da, beraz, puntu horietako bakoitzean higikariak izango duen aldiuneko abiaduraren norabidearekin. Ardatz honen norabidea izango duen
 bektore unitarioa definituko dugu.
bektore unitarioa definituko dugu. - Ardatz normala: aurrekoarekiko perpendikularra izanik, OA ibilbideko edozein puntutan ardatz hau kurbadura zentrorantz zuzenduta egongo da. Norabide honetan ere, definitu ahal izango dugu
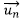 bektore unitario bat, kurbadura zentrora zuzenduta egongo dena uneoro.
bektore unitario bat, kurbadura zentrora zuzenduta egongo dena uneoro.
Gauzak horrela, aurreko atalean zehaztutako aldiuneko azelerazio bektorea, bi ardatz hauen arabera deskonposa dezakegu, ardatz horietako bakoitzarekin bat datozen osagaietako bakoitzari azelerazioaren osagai intrintseko izenez ezagutzen direlarik. Hau da:
![]()
![]()
Kontutan izanik azelerazioaren osagai intrintseko biak elkarzutak direla, aldiuneko azelerazioaren modulua kalkulatzeko beste bide bat ondorengoa izango litzateke:
![]()
Baina nola kalkulatu azelerazioaren osagai intrintseko bakoitzaren balioa? Azter dezagun kasu bakoitza banan-banan:
Azelerazioaren osagai tangentziala
Esan bezala, bektore honen norabidea eta noranzkoak bat datoz, OA arkuko edozein posiziotan higikariak duen aldiuneko abiadura bektorearekin. Bere moduluak, posizio bakoitzean, aldiuneko abiaduraren moduluak jasaten duen aldaketaren berdina da. Matematikoki adierazita:
![]()
Ondorioz:
![]()
Zer esan nahi du goiko adierazpenak? Une jakin bateko azelerazio tangentzialaren balioa kalkula ahal izateko beharrezkoa izango da, lehenik eta behin, abiaduraren moduluaren aldaketa denborarekiko nola ematen den zehaztea:
![]()
Lortutako adierazpena deribatu ondoren, azelerazio tangentzialaren aldakuntza denborarekiko azaldu duen adierazpena lortuko dugu
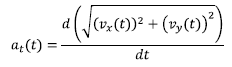
Lortutako adierazpenean, nahikoa izango da denbora une jakin baten balioa ordezkatzea, une horretako azelerazio tangentzialaren modulua kalkula ahal izateko.
Azelerazioaren osagai normala
Azelerazio normalaren moduluaren balioa bat dator, ardatz normalaren norabidean definituriko bektore unitarioaren aldakuntzarekin denborarekiko.
![]()
Goiko adierazpenaren ebazpen matematikoaren konplexutasun maila handia izanik, goazen adibide batean oinarritzea, azelerazio normalaren kalkulua gauzatzeko.
Horretarako, suposa dezagun abiadura zirkular uniformez higitzen den higikari bat.
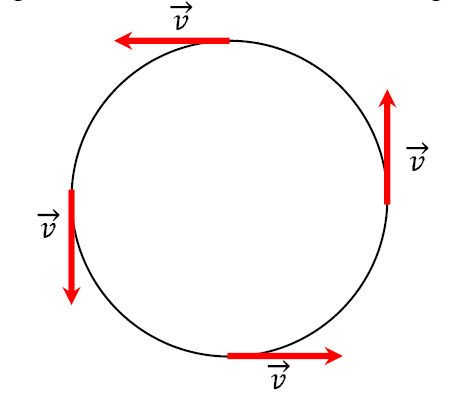
Irudika dezagun higikariaren posizio eta abiadurak, higidura horren bi denbora une desberdinetan:
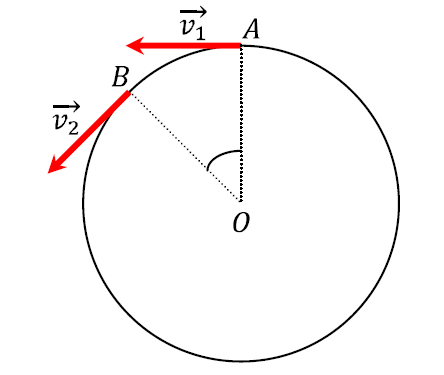
Bi denbora une desberdin horien arteko batez besteko abiaduraren irudikapena eginez:
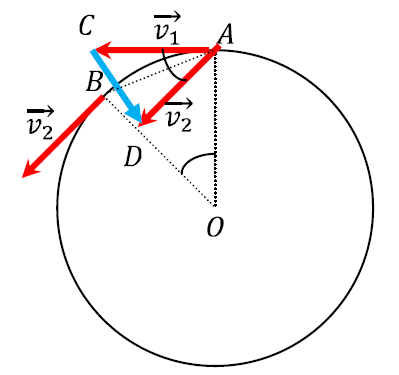
Irudiari arretaz begiratuz gero, antzeko bi triangelu isoszele ikusiko ditugu: AOB eta CAD. Antzekoak direla ziurta dezakegu ![]() betetzen delako. Antzekotasun irizpideetan oinarriturik, zera ziurta daiteke:
betetzen delako. Antzekotasun irizpideetan oinarriturik, zera ziurta daiteke:
![]()
Eta ondorioz:
![]()
Adierazitako zuzenki baten esanahi fisikoari erreparatuz:
- CD= batez besteko abiadura bektorearen modulua da:
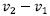
- AB= bi denbora une horien arteko desplazamendu bektorearen modulua izango da:
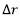
- AC=
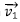 bektorearen moduluarekin bat dator:
bektorearen moduluarekin bat dator: 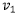
- OA= higikariak deskribatzen ari den ibilbidearen kurbadura erradioa da: R
Honen ondorioz, goiko adierazpena horrela geratuko litzateke:
![]()
Azelerazioaren definizio fisikoan oinarrituz (batez besteko abiaduraren eta denbora tartearen arteko proportzioa):
![]()
Moduluan:
![]()
Goran lortu dugun adierazpena ordezkatuz:
![]()
Planteamendu honen hasieran aipatu dugun bezala, higikariaren higidura uniformea dela suposatu dugu. Ondorioz:
![]()
Beraz:
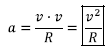
Beraz, higidura zirkular uniformean agertzen den azelerazio mota bakarra, abiaduraren norabide aldaketari dagokiona izanik, lortu dugun hori izango da, edozein ibilbide kurbakorrean higikariak izango duen azelerazio normalaren modulua.
Kontutan Hartzekoa
A) Nahiz eta egindako eskeman ez ikusi oso garbi, kontutan hartu behar da azelerazio normalaren norabide eta norantza bat datorrela ![]() bektorearen norabidearekin, eta hau, irduian ikusi daitekeenaren arabera, kurbadura zentrorantz zuzenduta dago, abiadura bektoreekiko normala izanik.
bektorearen norabidearekin, eta hau, irduian ikusi daitekeenaren arabera, kurbadura zentrorantz zuzenduta dago, abiadura bektoreekiko normala izanik.
Ebaztutako Ariketa
10.- Higikari baten posizioa ekuazio hauen bidez adierazten da:
- t=2 seg denean, kalkula ezazu:
- Abiadura.
- Azelerazioa.
- Ibilbidearen kurbadura erradioa. (Ebazpena – pdf, 200KB)
Proposatutako Ariketak
11.- Nola da posible, abiaduraren modulua konstantea duen higidura bat, mugimendu azeleratua izatea?. Ondo esplikatu.
12.- Adierazi ezazu ondorengo baieztapenak egiazkoak ala gezurrezkoak diren:
- “Edozein higidura kurbakorretan higikariak azelerazio normala du (an) baina ez azelerazio tangentziala (at)”
- “Higidura zuzen guztiek azelerazio tangentziala (at) aurkezten dute baina ez azelerazio normala (an)”
13.- Higikari baten posizioaren koordenatuak, denborarekiko, ondoko hauek dira:
![]()
- Kalkula ezazu, t=1 s denean.
- Abiadura bektorea eta bere modulua.
- Une bereko azelerazio bektorea eta bere modulua.
- Une horretako azelerazio tangentzialaren balioa.
14.- Higikari baten ekuazio parametrikoak ![]() eta
eta ![]() dira. Bila itzazu:
dira. Bila itzazu:
- Ibilbidearen ekuazioa.
- Mugikariaren posizioa hasieran.
- Higiduraren grafikoa egin.
- Hasierako abiadura.
- Azelerazioa eta bere osagaiak.
- Esplikatu ezazu zure hitzekin zein higidura mota den deskribatzen dena.