Orain arte osziladore harmonikoaren higiduraren azterketarekin aritu gara bere posizioa aldarazten duen kausa kontutan hartu gabe. Baina, Newton-en bigarren printzipioa aintzat hartzen badugu, HHS-a higidura azeleratua izanik behar beharrezkoa da tartean gorputzaren gainean eragiten duten indar guztien ordezkari bat egotea. Hauxen da, hain zuzen ere, saio honetan aztertuko duguna; zeintzuk dira HHS eragiten duten indarren ezaugarriak eta, jarraian, garrantzia berezia duten bi HHS-en azterketa dinamikoa egingo dugu, pendulua eta malgukia, hain zuzen ere.

Sarreran esan dugun bezala, kontutan izanik zeintzuk diren HHS-aren ezaugarriak, Newton-en dinamikaren oinarrizko printzipioa () bete beharko da. Kontuan hartzen badugu aurreko saioan lortu genuen adierazpena , zera dugu:

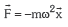
Osziladore harmoniko batentzat m eta ω konstanteak direnez, ondorengo espresioa lortzen da:

Ondorioz, HHS-rekin higitzen den partikula baten gainean eragiten duen indarra indar zentrala da (mugimenduaren zentrora zuzenduta beti eta honekiko mantentzen duen distantziarekiko proportzionala. Esan dezakegu, beraz, horrelako indar baten eraginez sortzen diren mugimenduak HHS-ak izango direla. Azter ditzagun bi kasu berezi:

Malguki Baten Oszilazioa

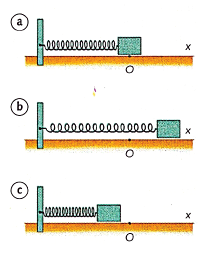Jo dezagun k konstante elastikoa duen, plano horizontal batean dagoen eta x ardatzaren norabidean edozein distantziaraino oszila dezakeen malguki bat dugula. Malguki horren mutur bat finko dago eta bestean m masako partikula bat lotuta dauka.

Gorputza oreka posizioan aurkitzen bada erraz uler daiteke ez dela inongo indarrik agertzen bere gainean eta, ondorioz, orekan aurkituko da (a irudia). Sistema honek ez badu marruskaduraren eraginik, objektua oreka posiziotik aldentzen dugunean, malgukiak indar bat egingo dio objektuari, Hooke-ren legearen arabera (b eta c irudiak), bezala adierazi daitekeena.

Newton-en bigarren legearen arabera:

Honen arabera ikus daiteke a eta x proportzionalak direla eta aurkako norantzakoak; beraz, malgukiari lotuta dagoen objektuak hhs bat deskribatuko du eta ondorioz:

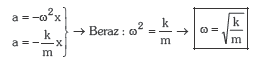
Oszilatzen ari den partikularen periodoa zera izango da:

Pendulu Baten Oszilazioa

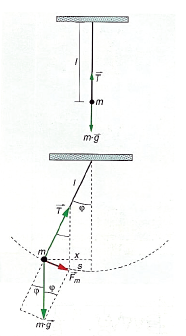Pendulu batek masarik gabeko l luzerako hari bat dauka. Honen mutur batetik m masako partikula bat zintzilikatzen da, beste muturra finko dagoelarik.

Lehenengo irudian oreka posizioan dagoen pendulu baten eskema ikus dezakezue. Egoera honetan m masaren gaineko erresultantea nulua da eta ondorioz ez da higidurarik izango.

Pendulua oreka posiziotik aldentzen badugu pisuaren osagai horizontala izango da mugimendua sortaraziko duena.: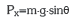

θ<5° bada, sinθ≈θ betetzen da eta ondorioz:·

Hau da:

(ikur negatiboaren esanahia indarrak x-en balioa murriztera jotzen duela da)

Azken adierazpen honen arabera, penduluan mugimendua sortzen duen indarra partikulak duen posizioarekiko proportzionala da eta aurkako norantzakoa. Newton-en bigarren printzipioa aplikatuz:

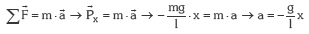
Hemen ere azelerazioa eta partikularen posizioa proportzionalak dira eta aurkako ikurra dute; ondorioz, ziurtatu dezakegu penduluak hhs bat deskribatzen duela.

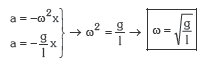
Oszilatzen ari den partikularen periodoa honako hau izango da:

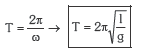
Kontutan hartzekoak

• Saio honen hasieran eman dugun 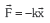ekuazioan agertzen den konstantea EZ DA malgukiaren errestituzio konstantea. K konstante hori proportzionaltasun konstante bat besterik ez da eta, orokorrean, adierazten dena ekuazio horretan horixe besterik ez da, osziladoreari eragiten dion indarra bere elongazioarekiko proportzionala dela. Malgukiaren kasu konkretuan bai etorriko da bat bere errestituzio konstantearekin baina beste HHS-etan beste balio desberdin bat izango du.
• Aurrean esan dugun bezala desbiderapen angelu txikientzat (θ<5°) penduluaren higidura zuzena kontsidera daiteke (IE bakarrik). Angelu txiki hauentzat angeluaren balioa radianetan eta beraien sinuen balioak ia berdinak dira, hurrengo taulan ikus daitekeen bezala:

α(º)	α(rad)	sinα	%
0	0	0	0
2	0,0349	0,0349	0
5	0,0873	0,0871	0,11
10	0,175	0,174	0,51
15	0,262	0,259	1,1

Ebaztutako Ariketa

9.- Masa berdineko bi gorputz k₁ eta k₂ konstanteak dituzten bi malguki independenteetatik zintzilikaturik daude. k₁<k₂ bada eta bien oszilazioek anplitude berbera badute, zein sistemak izango du abiadura maximorik handiena?. (Ebazpena, pdf-30,13 KB)

10.- Pendulu sinple baten luzera 25 cm-koa da eta bere periodoa 1 s-koa. Kalkulatu:

1. Lekuaren grabitatearen balioa
2. Penduluaren masa 15 g-koa bada, oreka posiziotik 30º desbideratzen bada, zenbat balioko du indar berreskuratzaileak posizio honetan?
3. Zein abiadurarekin pasako da oreka posiziotik?

(Ebazpena, pdf-32,45 KB)

Proposatutako Ariketak

11.- Penduluzko erloju bat doituta dago g=9,6720 m·s^-2-ko grabitatea duen leku batean. g=9,8123 m·s^-2-ko grabitateko beste leku batean ipintzen bada, zenbat atzeratu edo aurreratuko da egun bakoitzean?

12.- 1 kg-ko bloke bat k=25 N/m-ko konstante elastikoa duen malguki batetik zintzilikatzen da. Bloke hori 10 cm beherantz eramaten badugu eta gero aske uzten bada:

1. Zer abiadurarekin igaroko da oreka posiziotik?
2. Zein da burutzen dituen oszilazioen periodoa?

Webgune Interesgarriak

• Galileoren pendulua: Pendulu erlojuaren asmakuntza Galileori zor diogu. Artikulu honetan Pisako katedralean burutu zituen esperientzien berri izan dezakezue