Higiduraren deskribapena

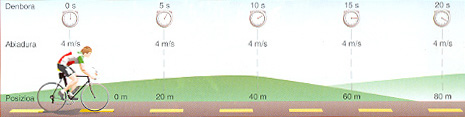
Adibidean ikusten denaren arabera, higidura zuzena da higikariak deskribatzen duen ibilbidea zuzena delako. Honetaz gain, bere abiadura konstantea mantentzen du modulu, norabide eta noranzkoan. Horrelakoetan higidura hori zuzen eta uniformea dela esaten da.

Aurreko unitatean ikusi dugu azelerazioarn osagai normalak abiaduran gertatzen diren norabide aldaketak adierazten dituela. HZUan ibilbidea zuzena denez, abiadura ibilbidearekiko ukitzailea da beti eta ez du bere norabidea aldatzen. Beraz, azelerazioaren osagai normala zero da (A).

Bestalde, azelerazio tangentziala abiaduraren moduluaren aldaketarekin bat datorrenez, bere balioa ere nulua izango da.

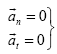Ondorioz:

Higidura zuzen uniformearen berezitasuna azelerazioaren osagai biak zero izatea da. Azeleraziorik gabeko higidura da.

Higiduraren ekuazioa

HZUaren kasuan, atezbesteko abiadura aldiuneko abiaduraren berdina da denbora guztian. Bere adierazpen matematikoari erreparatuz:

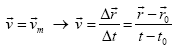
Aurreko adierazpenean  bakanduz, higiduraren ekuazio bektoriala lor dezakegu:

            

Higidura zuzen uniformea denez, erreferentzi sistema modura higiduraren norabideari dagokion OX ardatza har dezakegu, aurreko adierazpena honela jar dezakegularik:

Erreferentzi sistema horretan, bektore guztiek norabide bera dute. Beraz, higiduraren ekuazioa modu eskalarrean adieraz dezakegu:

 eta ondorioz:  (B)

Ekuazio hori beste era askotan adieraz daiteke (eta normalean adierazten dira). Ikus ditzagun kasu ezbedinak:

1. Higikariaren desplazamenduan noranzkoaren aldaketarik ematen ez bada, denbora tarte jakin batean egindako desplazamendua bat etorriko da ibilbidearekin. Hori dela, kasu honetan bakarrik, adierazpen bektoriala horrela jar genezake: 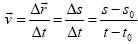 eta ondorioz,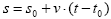
2. Bestalde, aukeratutako erreferentzi sistemaren jatorria higikariaren hasierako posizioarekin koinziditu arazten badugu (s₀=0), higikariak deskribaturiko bidea bat etorriko da (t-t₀) denbora tartean v abiaduraz egin duenarekin. Ondorioz:
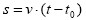
3. Erreferentzi sistema aukeratu eta edozein lekutan koka dezakegun moduan, denbora zein unetan hasten garen neurtzen ere aukeratu dezakegu. Horrela, zero balioa higidura hastera doanuneari eman diezaiokegu. Eta une bakoitzean igarotzen den denbora t izango da, t₀=0 delako. 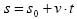 edota 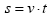 baldin eta erreferentzi sistemaren eta higiduraren jatorriak bat badatoz. (C)

Higiduraren grafikoak

Jadanik ikasita daukagunez, higiduren azterketa grafikoa egiterakoan, denborarekiko (hau da, aldagai askearekiko) aldatzen diren beste parámetro zinematiko guztien (menpeko aldagaien) aldakuntza nola ematen den behatuz, higiduraren deskribapena egiteko aukera izaten da. Beraz, higidura mota honen adierazpen grafikoek posizioa/denborarekin, abiadura/denborarekin edota azelerazioa/denborarekin jarriko dute harremanetan, horrela x/t, v/t edota a/t bezala ezagutzen diren grafikoak aztertu beharko ditugularik.

• a/t grafikoa:

a=0 denez, funtzio nulua izango dugu.

• v/t grafikoa:

v=konstantea denez, funtzio konstantea izango da, hau da, zuzen horizontala. Abiadurak izango due ikurraren arabera, hau abzisaren gainetik edo azpitik marraztu beharko da.

• x/t grafikoa:

Posizioaren ekuazioa denborarekiko funtzio afina da , beraz, bere adierazpen grafikoa zuzen batena izango da. Zuzen honen ezaugarriak x, x0 eta v parametroek hartuko duten balioa eta euren zeinuaren araberakoa izango da. Kasu bakoitzean grafikoa interpretatu eta higiduraren ezaugarriak adieraztea izando da gure helburuetako bat. Bestea, grafikoan oinarrituz, higiduraren ezaugarri desberdinak zehaztea.

Kontutan hartzekoak

A) Zuzen bat erradio infinitua duen zirkunferentzia bat dela kontuan izanik, ondorio berera heltzen gara, azelerazio normala kalkulatzeko erabiltzen dugun adierazpenaren bitartez:

Kontutan izanik  izango da.

B) Kontutan izan behar da, ekuazioan adierazten diren magnitude bektorial guztiek (posizioa eta abiadura) norabide berbera dutela baina noranzkoa desberdina izan dezaketela. Eta zer ondorio du honek ekuazioan?. Bada, magnitude horiei euren balioak atxikitzerakoan zeinu positiboa nahiz negatiboa eduki ahal dezaketela et horrelaxe txertatu beharko ditugu ekuazioan emaitza egokiak lortu ahal izateko.

C) Azken bi ekuazioak ibilbide zuzenarekin ematen ez diren higiduretan ibilitako distantzia kalkulatzeko erabiltzen dira ere, baldin eta abiaduraren modulua konstantea bada, noski

Proposatutako ariketak

1.- Gelara sartu aurretik, Leire eta Sara etxerako lanetan lorturiko emaitza baten inguruan eztabaidatzen topatu nituen aurreko batean. Kontua da, Higidura Zuzen eta Uniformea zeraman higikari baten abiadura kalkulatzerakoan, Leireri abiaduraren balioa negatiboa atera zitzaiola eta emaitza gaizki zeukalakoan zegoen. Sararen iritziz, abiadura negatiboa izateak esanahi fisikoa bazuen; halere, Leirek ez zeukan oso garbi hori horrela izatea posiblea ote zen. Zer deritzozu zuk? (TW21)

2.- Ondorengo grafikoak higidura zuzen baten eboluzioa azaltzen du.

Kalkulatu:

1. Tarte bakoitzeko abiadura
2. Zein da batezbesteko abiadura?
3. Zein da batezbesteko abiadura lehenengo lau segundotan?
4. Zein da aldiuneko abiadura 5. segundoan?

3.- Higikari baten posizioa denborarekiko ondoko grafikoan adierazten da.

Kalkulatu:

1. Abiadura adierazitako tarte bakoitzean.
2. Higikariaren desplazamendua
3. ibilitako espazio osoa (suposatuz higidura zuzena dela)
4. Egizu adierazten den denbora tarte bakoitzeko v/t grafika

4.- Abuztuaren 27an jokatu zen lehen euskal derbian, Errealak banako berdinketa lortu zuen Athletic-en aurka, Mikel Aranburuk  86. minutuan sartutako gol bati esker. Jokaldia Mikel Alonsok ,arrasean, alboko marraren norabidean, egindako jaurtiketa batekin hasi zen, baloiari 27 km/h-ko abiadura eman ziolarik. Mikel Alonso baino 10 m atzerago aurkitzen zen Xabi Prieto, korrikan hasi zen baloiaren bila,  jaurtiketaren norabide berean. Bere abiadura 36 km/h-koa zen. Zer distantzia korritu zuen Prietok baloia harrapatu arte? Zenbat denbora behar izan zuen horretarako?