Unibertsoaren eredu heliozentrikoa onartzen bada, Keplerren legeek esanahi zinematikoa baizik ez dute: planeten higidurak deskribatzen dituzte soilik, baina ez dute sortarazten duen arrazoia azaltzen. Newton-ek emandako GRABITAZIO UNIBERTSALAREN LEGEAren bitartez, Keplerren legeei esanahi dinamikoa gehitzen zaie, higidura hauen kausa bezala indar kontzeptua barneratuz. Dinamikaren bere legeak aplikatuz eta Keplerren legeak kontutan harturik, Newton-ek frogatu ahal izan zuen planeta bati Eguzkiaren inguruko orbitan eusten dion indar zentrala txikiagotu egiten dela planeta honen eta Eguzkiaren arteko distantzia handiagotzean eta bestalde planetaren masarekiko proportzionala dela.

Lurrak orbitan irauten du Eguzkiaren erakarpen indarrak eragozten diolako ukitzailetik irtetera, hau da, bere abiaduraren norabidearen aldaketaren ondorioz agertzen den indar zentrifugoari kontrajartzen zaio, inertzi printzipioaren ondorioz gertatu behar den bezala.

Kalkuluak erraztearren. Newton-ek, orbiten eszentrizitatea txikia dela eta, orbita planetarioak zirkularrak kontsidera daitezkeela suposatzen du. Ondorioz, abiadura lineala eta areolarrak konstanteak izango dira.

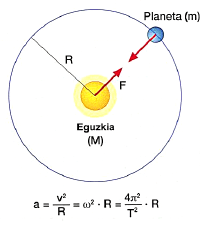Esandakoaren arabera, Eguzkiaren erakarpen indarra honela adierazi daiteke:

eta izanik:

Beraz:

Kontutan hartuz planetaren periodoa Eguzkiaren inguruan dela:

Keplerren hirugarren legearen arabera da, k₁ planetaren masarekin aldatzen ez den konstantea izanik. Aurrekoan ordezkatuz:

Indar zentripetu hau, Eguzkiak planetaren gain “urrutitik” eragiten duela onartzen bada, planetak, akzio-erreakzioaren printzipioaren arabera, Eguzkiaren gain balio berdina baina aurkako norantza duen indarra eragingo du. Aurreko arrazonamenduarekin parekatuz, indar horren balioa ondokoa izango da:

non M Eguzkiaren masa eta k₂ masa honekin aldatzen ez den konstantea diren.

Bi indar hauek aurkako norantzakoak dira baina balio absolutu berbera dute. Hau da:

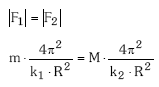
Sinplifikatuz:

eta ondorioz:

Beraz, direnez, dagozkien erakarpen indarraren adierazpenean ordezkatuz:

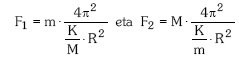
Aurrean aipatu den bezala, bi indar hauek balio absolutuan berdinak dira bi adierazpen horiek batean laburtu daitezkeelarik:

zatiduraren balioa konstantea da eta GRABITAZIO UNIBERTSALAREN KONSTANTEA (G) deitzen zaio, bere balioa S.I.ean 6,67·10^-11 N·m²·kg^-2 delarik.

Beraz:

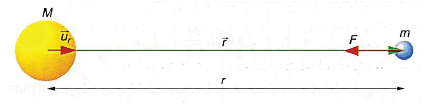
Ekuazio honek Eguzkia eta planetaren arteko erakarpen indarra adierazten du. Astroez gain, Unibertsoan dauden gorputz guztientzat eremu grabitatorio bat dagoela onartzen bada, ondorioztatutako ekuazio honek enuntziatu orokorrago batera eramaten gaitu:

Edozein bi gorputzen arteko erakarpen indarra, beren masen biderkadurarekiko zuzenki proportzionala eta grabitate zentroen distantziaren karratuarekiko alderantziz proportzionala da.

Lortu dugun adierazpena bektorialki honela adierazi beharko litzateke:

Proposatutako Arietak

2.- G konstantea unibertsala denez, hauxe esan dezakegu:

1. Masa batek sortzen duen grabitazio eremua berdina da espazioaren puntu guztietan.
2. Masa batek sortzen duen grabitazio eremua ez da gorputz hori inguratzen duen ingurunearen araberakoa.
3. Masa batek sortzen duen grabitazio eremua gorputz hori inguratzen duen ingurunearen araberakoa da.
4. Aurreko baieztapenetatik gutxienez bi egiak dira.

3.- Lurra ez da beti abiadura berdinez higitzen Eguzkiaren inguruan. Adierazi zein gunetan higitzen den Lurra abiadura handiagoz: afelioan, perihelioan edo tarteko puntu batean. Justifikatu zure erantzuna ondorengoa erabiliz:

• Keplerren bigarren legea.
• Grabitazio eremuaren teoria.

4.- Berdinak diren bi satelite artifizial Lurraren inguruan biratzen ari dira erradio ezberdineko bi orbitetan. Bietatik zein higituko da abiadura handiagoarekin?, Zergatik?.