Orokorrean, m masa duen gorputz baten gainean eragiten duten indarren erresultantea ezagutuz gero, gorputz hori zein azelerazioz higitu eta, ondorioz, zein higidura mota duen zehaztu dezakegu. Ikusten denez:

Indar erresultantea aldatzen ez bada, puntuaren higidura zuzena eta uniformeki azeleratua izango da

Higidura azeleratuaren adibide garbi bat (batzuek egunero jasan behar izaten dutena) igogailu batek, martxan hasten denetik gelditzen denera arte, egiten duena da. Lekuren batera igotzeko igogailua erabiltzen dugunean, higitzen hasten den momentuan badirudi lurzorua gogor zapaltzen dugula gure oinekin. Igogailuaren barruan komunetan edukitzen dugun pisu bat jartzen badugu eta gainean jartzen bagara, igogailua igotzen hasten den unean gehiago “pisatzen” dugula ikusiko dugu. Nola azaldu balantzak adierazten duen “gehiegizko pisu hori”?

Erreferentzi sistema ez-inertzialak

Azaltzeko, kontuan izan behar dugu baldintza horietan igogailua ez dela erreferentzi sistema inertziala, azeleratua dagoelako. Erreferentzia-sistema inertziala Newtonen legeak betetzen diren erreferentzia-sistema da. Horretarako, aurretik inertzialtzat hartu den sistema batekiko azelerazio nuluan joan behar du (lerro zuzenean abiadura konstantean edo nuluan). Azelerazioa badago beste sistema horrekiko, tangentziala edota normala, ez-inertziala izango da.

Horrela, igogailuaren adibidean, igogailua bera erreferentzia sistema inertziala dela suposa dezakegu, bere igoera edo jaitsiera abiadura konstantea mantentzen denean. Egoera horretan, komuneko pisuak gure gorputzaren benetako pisua adieraziko du nahiz eta igogailua mugimenduan egon. Igogailua abiatu edo gelditzen denean azelerazio baten eraginez gertatzen da eta ondorioz, erreferentzi sistema ez-inertzial batetan egongo ginateke. Sistema ez-inertzialen aurrean gaude…

• … erreferentzi sistemaren abiaduraren moduluan aldaketa bat ematen denean (azelerazio tangentziala).
• … erreferentzi sistemaren translazio abiaduraren norabidean aldaketa bat ematen denean (azelerazio normala).
• … erreferentzia sistemaren errotazioa ematen denean bere puntu konkretu batekiko.
• .. aurrekoen konbinazioa den egoera bat gertatzen denean.

Sistema ez-inertzial hauetan gertatzen diren mugimenduak aztertzerakoan, zein den behatzailearen posizioa, alegia, sistema ez-inertzialaren barnean ala honekiko kanpokoa den, zehaztea oso garrantzitsua da. Izan ere, sistema ez-inertzialetik kanpo dagoen behatzaile batentzat (erreferentzi inertzial batean egongo dena) Newtonen legeak aplikatuz, sistemaren azelerazioa kalkulatuko dugu ohi bezala. Baina behatzailea, sistema ez-inertzialaren barnean kokatzen bada, Newtonen legeak betetzeko, “indar misterioso” baten presentzia kontutan hartzea derrigorrezkoa izango litzateke. Indar irudikari hauek ez dira existitzen, ez baitira beste gorputz batekin gertatzen den interakzioaren ondorioa, baina aintzat hartzera derrigortuta gaude sistema ez-inertzialetan gertatzen diren fenomenoak, Newton-en printzipioen bitartez azaldu nahi baditugu.

Sistema ez-inertzialen adibideak

1. Igogailua

   Suposa dezagun gorantz desplazatzen ari den igogailu bat. Igogailua geratzerakoan galgatze indar bat aplikatzen da bere gainean, desplazamenduaren aurkako noranzkoa duen azelerazio bat eragiten delarik. Egoera horretan igogailuan dagoen pertsonaren pisua neurtuko bagenu, konturatuko ginateke bere “itxurazko pisua” benetakoa baino txikiagoa dela. Nola kalkulatu pisu hori, behatzailea igogailutik kanpo (sistema inertzialean) edo igogailuaren barnean (sistema ez-inertzialean) dagoen kasurako?

   Behatzaile inertziala

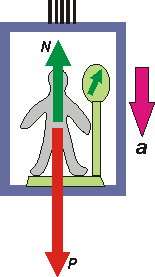   Orain arte egin dugun moduan, oraingoan ere Newtonen printzipioak beteko direla suposatuko dugu. Alegia, igogailuan doan pertsonaren gainean eragiten duten indar guztien erresultanteak bere gainean agertzen den azelerazioa eragingo du.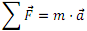

   

   

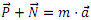
   Igogailuaren higiduraren azelerazioa eta sistemako indarren noranzkoak aintzat harturik, moduluen arteko erlazioa ondorengoa izango da:

   

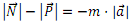
   Horrela, pertsonaren itxurazko pisua, alegia, komuneko pisuaren aurka egiten den indarra (honek, erreakzio bezala, oposatzen duen indar normalaren berdina izango dena) ondorengoa izango litzateke:

   

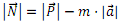
   Behatzaile ez-inertziala

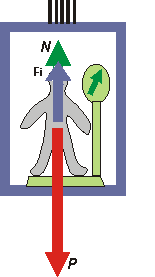   Igogailuaren barnean erreposoan dagoen behatzaile batek, igogailua geratzen ari den bitartean, bere gainean eragiten duen indar “misterioso” bat nabaritzen du. Bere oreka egoera justifikatzeko, hau da, Newtonen printzipioak betetzeko, indar ez-inertzial baten presentzia dagoela onartu beharko genuke. Horrela, igogailuan dagoen pertsonaren gainean ageri diren hiru indarren ordezkaria nulua izan beharko da.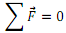

   

   

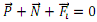
   Aurreko adierazpena moduluaren arabera:

   

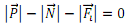
   Kasu honetan, komuneko pisuak antzemango duen itxurazko pisuaren adierazpena ondorengoa izango litzateke:

   

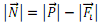
   Igogailuaren barnean doan pertsonaren gaineko indar inertzialaren modulua, igogailuak jasaten duen dezelerazioarekiko proportzionala izango da. Ondorioz:

   

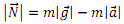
2. Higidura zirkularra

   Higidura zirkular guztietan abiadura bektorearen norabidearen aldaketa eragiten duen/duten indar bat/batzuk ageri da/dira. Norabide aldaketa horren ondorioz, sistema horrek azelerazio bat jasaten du. Beraz, higidura zirkularrez higitzen den sistema bat, sistema ez-inertziala da baita ere. Igogailuaren kasuan bezala, sistema honen azterketa dinamikoa modu ezberdinetara egin beharko genuke behatzailea sistema ez-inertzial honetatik kanpo edo barnean dagoela kontsideratuta. Nahiz eta higidura mota honen azterketa dinamikoa hurrengo atalean egin, azter dezagun modu deskriptibo batean, bederen, sistema ez-inertzial hau.

   Behatzaile inertziala

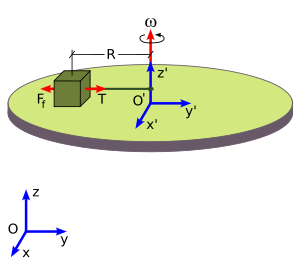   {O, x, y, z} erreferentzi sistema inertzialean kokatutako behatzaile batentzat gorputzaren higidura zirkularraren eragile bakarra sokaren tentsioa da (suposa dezagun marruskadura indarrik gabeko gainazal batean higitzen ari dela gorputza). Indar hori izango da, beraz, gorputzaren abiadura linealaren norabidearen aldaketa eragingo duena eta, ondorioz, azelerazio normalaren (edo zentripetuaren) eragile bakarra.

   Behatzaile ez-inertziala

   {O’, x’, y’, z’} erreferentzia sistema ez-inertzialean gainean higitzen ari den behatzaile batek berriz, biraketa gertatzen den bitartean, sistemak “ihes egiteko joera” (aurrean aipatutako indar misterioso hori) duela antzematen du. Sistema ez-inertzialak gainazalaren gainean duen biraketa mantentzea nahi bada, soka baten bitartez lotu beharko da biraketaren ardatzera. Horrela, sokaren tentsioa kanporantz agertzen den indar ez-inertzialaren (indar zentrifugoaren) berdina izango dela jabetuko da. Bi hauek modulu bera duten bitartean, sistemak bere biraketa mugimenduarekin jarraituko du.

Proposatutako ariketak

7.-Hasieran erreposoan dagoen kamioi batek 20 m/s-ko abiadura lortzen du 10 s-tan. Zein izan behar da kamioiaren eta zoluaren marruskadura koefizientearen balioa, atzean daraman kaja bat irrista ez dadin?

8.-Kaxa bat, kamioi baten zoruaren gainean aurkitzen da, geldiunean, kamioia 100 km/h-ko abiaduraz higitzen den bitartean. Kaxaren eta kamioiaren arteko marruskadura koefizientea =0,4 da. Bat-batean, gidariak balaztatu egiten du uniformeki kamioia gelditu arte (azelerazio konstantea). Lor bedi kamioiak egin dezakeen ibilbidearen luzerarik txikiena, gelditzeak irauten duen bitartean, kaxa horrek irrist egin ez dezan.

9.-Zenbatekoa izan beharko da grafikoko karrotxoaren azelerazio minimoa B blokea eror ez dadin? (Bien arteko marruskadura koefizientea  da)