a irudia:

Alboan ikus daitekeen irudian, higikari bat pasatu deneko puntuak adierazi dira. Puntu horiek deskribaturiko kurbari ibilbidea deritzo.

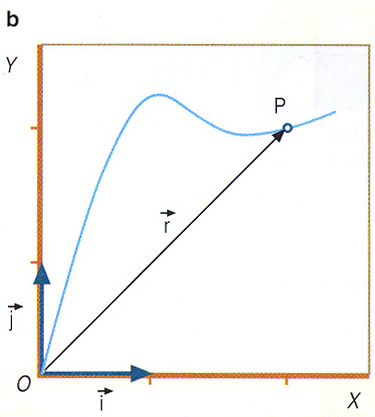
Ibilbide horretako P puntuaren posizioa determinatzeko, OX eta OY ardatzek eraturiko erreferentzi sistema aukeratu dugu.

 

b irudia:

Jatorriarekin batera P puntuak  bektorea determinatzen du. Horixe izango da une jakin horretan, higikariaren posizio-bektorea. Bere adierazpen matematikoa ondorengoa izango da:

Bektoreekin eragiketak egiterakoan, hauen adierazpena zertxobait aldatzea komeni da: horretarako nahikoa da bektorearen modulua bere norabide bera duen bektore unitario batekin biderkatzea. Beraz:

Ondorioz:

Beraz:

• MODULUA: 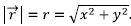. SI sisteman posizio bektorearen unitatea metroa (m) izango da
• NORABIDEA: bere bi osagaien araberakoa izango da
• NORANZKOA: bere bi osagaien araberakoa izango da. Posizio bektorearen kasuan, magnitude bektoriala den unetik, garrantzitsua izango da duen ikurra garbi zehaztea. Honen arabera noranzko bat edo bere aurkakoa adierazi baitezakegu.

Denboran zehar, higikariak posizio ezberdinak izango ditu. Ikuspegi matematiko batetik zera esan dezakegu: posizio bektorea (menpeko aldagaia) denboraren (aldagai askea) menpeko funtzioa dela. Hau da,  bezala adieraz daiteke.

Higikariak denboran zehar duen posizioa deskribatzen duen ekuazioari higiduraren ekuazioa deritzo eta horrela adierazten da:

Posizio-bektoreak denboraren funtzioan dituen osagaiei, ibilbidearen ekuazio parametrikoak deritze:

Aurreko ekuazioetatik t parametroa ezabatzen badugu (ekuazio sistema sinple bat ebaztuz), ibilbidearen ekuazioa lortuko dugu. Hau da, benetako ibilbideari (edo kurbari) erantzuten dion ekuazio matematikoa, aldagai bakarrak x eta y osagai kartesiarrak izanik.

Beste era batean esanda: lortutako funtzio matematikoaren adierazpen grafikoa bat dator higikariak deskribatutako ibilbidearekin.

c irudia:

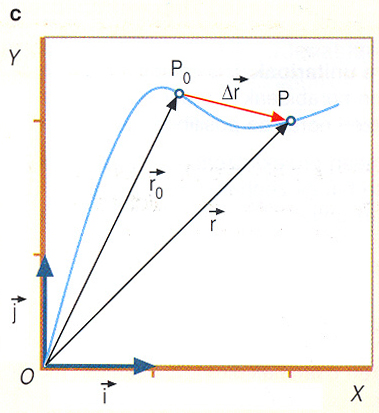
Higikariak egindako ibilbideko bi puntu, P0 eta P, bektore batez biltzean, bi puntuen arteko desplazamendu-bektorea lortuko dugu. Aurreko atalean ikusi dugun bezala, desplazamendu bektorea  jatorria P₀ puntuan eta muturra P puntuan duen bektorea da. Bektore hau kalkulatzeko,  posizio-bektorearen eta  posizio-bektorearen arteko kendura egin behar da:

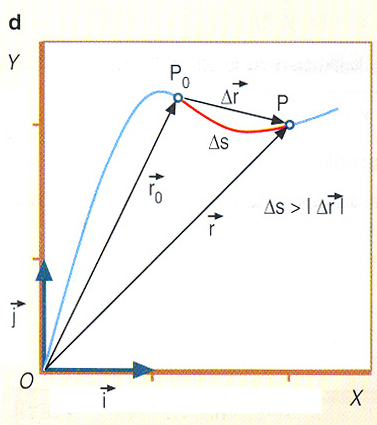d irudia:

Ibilbidea zuzena denean, eta higiduran noranzko-aldaketarik ez dagoenean, desplazamendu-bektorearen modulua, , higikariak ibilbidearen gainean egindako distantziaren, , berdina da.

Bestelako kasuetan, higikariak ibilitako distantzia, , desplazamendu-bektorearen modulua, , baino handiagoa da.