Jo dezagun soka luze bat dugula eta sokaren mutur batean oszilazio bat sortzen dugula. Oszilazio hori, denborarekin, sokaren beste puntuetara iritsiko da. Azkenik, sokaren puntu guztiak arituko dira modu berean oszilatzen. Sokan zehar uhina hedatu egin dela esango dugu.

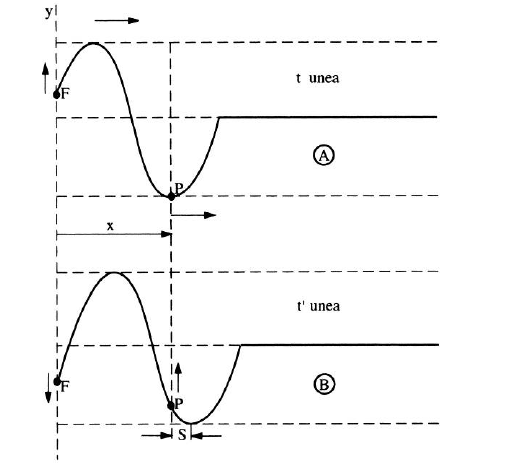
Ondorengo irudian dituzu soka batean hedatzen ari den uhinaren bi une desberdinetako egoerak.

A irudian, uhina P puntura iritsi da eta P puntua bera hasten da F puntuak duen oszilazioa (hau da, hhs-a) egiten. Uhina eskuinerantz ari da hedatzen sokako puntuak bertikalki oszilatzen duten bitartean.

B irudian, geroagoko egoera adierazi nahi da. Bertan uhinak A-rekiko eskuinerantz s distantzia bat egin du, P puntua gorantz abiatu da eta F, aldiz, beherantz doa.

Orain esandakoaren arabera, bi higidura izango dira, beraz, kontuan hartu beharrekoak:

• UHINAREN HEDAPENA: kasu honetan eskuinerantz. Higidura zuzen eta uniformea da.
• UHINAREN PARTIKULEN OSZILAZIOA: kasu honetan bertikala. Higidura harmoniko sinplea da.

Uhinaren ekuazioa edozein puntutan sortutako higidura harmonikoaren ekuazioa da.

• FOKUAren higiduraren ekuazioa: 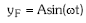(suposatuko dugu fokua oreka posizioan hasten dela oszilatzen)
• P PUNTUAK ere higidura harmonikoa du. Beraz:

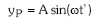
t’, P puntua bibratzen hasi denetik pasatutako denbora da eta t, fokua emititzen hasi denetik pasatutakoa. Zer esanik ez, t’ t baino txikiagoa dela, uhinak P puntura iristen denboraren bat behar izan du eta.

Jo dezagun uhina v abiaduraz hedatzen dela eskuinerantz. Beraz, F-tik P-ra joateko behar duen denbora   izango da. Ondorioz, P puntuak bibratzen daraman denbora izango da, hau da,  .

Ekuazioan ordezkatuz:

Kontutan izanik :

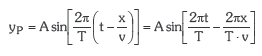
izanik:

Ondorioz:

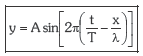
Denbora kontatzen hasten garen unean perturbazioak fokuan θ₀ fasea badauka (hasierako fasea) aurreko adierazpena honela geratuko zaigu: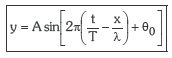

Funtzio honek fokutik x distantziara dagoen puntu batek t une jakin batean duen elongazioa adierazten du, hau da, x eta t-ren funtzioa da (y(x,t)). Ondorioz, uhinaren ekuazioa BI ALDIZ PERIODIKOA da, izan ere, sinu funtzioa funtzio periodikoa denez, periodikoa da posizioarekiko eta denborarekiko:

• x=ktea bada: funtzioak perturbazioa puntu batean nola aldatzen den adierazten digu.

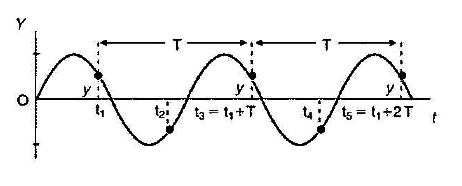
• t=ktea bada: une jakin batean inguruneko puntu guztien bibrazio egoera ematen digu.

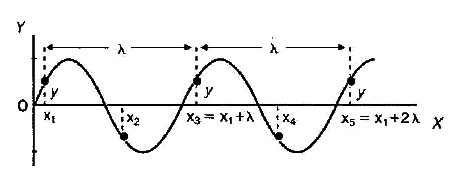
gaiari uhinaren FASEA deritzo, bere balioak t aldiunean x puntu baten bibrazio egoera zehazten baitu. Ondorioz, uhinaren bi punturen arteko FASE DIFERENTZIAK puntu horien bibrazio egoeren arteko diferentzia adierazten digu.

• Uhin bereko bi puntu FASEAN daudela edo FASE KONKORDANTZIAN daudela esan ohi da, edozein aldiunetan puntu horietako bibrazio egoera berbera denean. Kasu honetan bien arteko fase diferentziak 2nπ balio du, n∈Z izanik.
• Uhin bereko bi puntu AURKAKO FASEAN edo FASE OPOSIZIOAN daude edozein aldiunetan puntu horien bibrazio egoerak elkarren aurkakoak direnean. Hau gertatzen da baldin eta bien arteko fase diferentzia (2n+1)π bada, n∈Z izanik.

Kontutan hartzekoak

• KONTUZ!. Ez dira nahastu behar uhinaren HEDAPEN ABIADURA eta inguruneko puntu baten BIBRAZIO ABIADURA. Lehenengoan higidura uniformea batetaz ari gara eta bigarrenan higidura harmoniko sinpleaz.
• Ondorengo planteamenduan honakoa onartu da: alegia, erreferentzi sistema bateko ardatz batean, positibotzat hartutako norantzan higitzen dela, hau da, eskuinerantz. Kasuren batean, uhina negatibotzat hartutako norantzan higituko balitz, hau da, OX ardatzaren ezkerrerantz, uhin ekuazioa 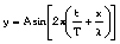izango litzateke.

• Zenbait kasutan ekuazio honen baliokidea den beste bat erabiliko dugu:

eta direnez:

Ebaztutako Ariketak

1.- Zeharkako uhin bat soka batean hedatu da honako ekuazioaren arabera:
        y(x,t)=0,4cos(50t-2x)
Ekuazioa Sistema Internazionaleko unitateetan dago adierazita. Kalkulatu:

1. Uhinaren hedapen abiadura.
2. t=0,5 s denean fokutik 20 cm-ra dagoen partikula baten bibrazio egoera. (Ebazpena, pdf-29,75 kb)

Proposatutako Ariketak

Ariketekin hasi baino lehen ohar pare bat. Lehenik eta behin, ariketan planteatzen den egoera zein den identifikatzea gomendatzen dizut. Ondoren ariketa behar den moduan planteatu, justifikatu eta azkenik, noski, matematikoki ebaztu, emaitza zuzena lortuz. Beraz, ez dira onartuko garapen eta ebazpide matematiko hutsak, Fisikaren puntutik eman daitezkeen azalpen edo justifikaziorik gabe. Ahalegin berezia ipini behar duzu ondorengo ataletan:

• Ariketa eta galderen garapenaren planteamendu eta justifikazio zuzentasunean
• Fisikaren legeen identifikazio eta erabilera zuzenetan
• Pausoz pausoka eginiko garapen, marrazki eta eskemen erabilpenean
• Oinarrizko kontzeptuen azalpena eta beraien aplikazio zuzenean
• Unitateen erabilera zuzenean

2.- Adierazi ezazu ondorengo baieztapenak egia ala gezurra diren, zure erantzuna arrazoituz: "Uhin harmoniko baten hedapen abiadura bere periodo eta anplitudearen menpe dago"

3.- Ondorengo grafikoek uhin baten higidura adierazten dute:

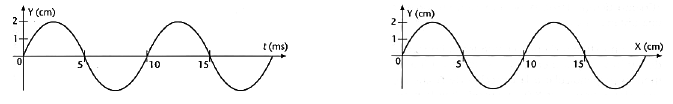
Lehenengo irudian desplazamendua, y, denborarekiko adierazi dugu posizio jakin baterako; bigarrenean, ostera desplazamendua posizioarekiko, t, une jakin baterako.

1. Adierazi ondorengo parametroen balioak:
• Anplitudea
• Uhin-luzera
• Maiztasuna
• Periodoa
• Pultsazioa
• Uhin zenbakia
2. Kalkulatu uhinaren hedapen abiadura.
3. Idatzi uhinaren hedapen ekuazioa.

4.- Uhin bat 3 m/s-ko abiaduraz higitzen ari da. Bere maiztasuna 2 Hz-koa da eta anplitudea 5 cm-koa. Hasierako unean, jatorritik 10 cm-ra dagoen puntu baten elongazioa 0 bada, bilatu uhin honen ekuazioa.

5.- Uhin bat 32 m/s-ko abiaduraz hedatzen da. Anplitudea 2,3 cm da eta maiztasuna 60 Hz. Hasierako unean elongazioa maximoa dela suposatuz, ondokoa galdetzen da:

1. Higiduraren uhin luzera
2. t=2,6 s denean jatorritik 51,2 m-ra dagoen puntu baten elongazioa, abiadura eta azelerazioa.

6.- 5 m-ko erradioa duen putzu zirkular baten zentroaren gainazalean uhin-higidura sortzen da. Ikusten denez, uhinek 10 segundo behar dituzte ertzera heltzeko eta elkarren jarraiko bi gailurren arteko distantzia 50 cm da. 1/6 segundo igaro ondoren, foku igorlearen elongazioa 3 cm-koa dela jakinik, kalkula ezazu higiduraren periodoa, maiztasuna eta anplitudea. Kalkulatu, azkenik, 8 segundotan foku igorletik 3,875 m-ra dagoen puntu baten elongazioa.

7.- Uhin baten ekuazioa y=25sin(0,4t-1,25x) da, x eta y cm-tan eta t s-tan daudelarik. Bilatu:

1. Hedapen abiadura
2. Maiztasuna
3. Uhin-luzera
4. Fasean eta aurkako fasean dauden puntuak.
5. Fokutik 5 cm-ra dagoen puntu batek, zein unetan izango du bibrazio abiadurarik handiena?.
6. Ezaugarri berdinak dituen eta aurkako norantzan hedatzen den uhin baten ekuazioa

8.- Soka baten muturrak y=2sin30&pit ekuazioa duen higidura harmonikoa du, anplitudea cm-tan eta denbora s-tan adierazita daudelarik. Sokan zehar higidura hau 2 m/s-ko abiaduraz hedatzen da.

1. Marraztu sokaren egoera t=0,5 s denean.
2. Muturretik 10 cm-ra dagoen sokako puntu baten higiduraren ekuazioa kalkulatu.