Higidura parabolikoa sortzen da gorputz bat lurretik hasierako v₀ abiaduraz eta horizontalarekin θ angelua osatzen duen norabide batez botatzen dugunean eta jaurti ondoren, gorputza aske gelditzen denean.

Hasieran gorputza jaurtitzen dugun norabidean abiatuko da, baina bere pisuaren eraginez ibilbidea aldatu eta azkenerako erori egingo da. Higidura hori aztertzeko, aireak higidurari egiten dion marruskadura indarra nulua dela pentsatuko dugu eta horrela, kalkuluak asko erraztuko ditugu.

Higidura hau bi higidura sinpleren konposizioa da:

• HZU horizontal bat, v_x abiadura konstanteaz.
• HZUA bertikal bat, goranzko hasierako abiadura v_0y izanik.

ABIADURA BEKTOREA

Hasierako abiadura () bere bi osagaietan deskonposatzen da, horizontala () eta bertikala(). Horien balioak erraz kalkula daitezke hasierako abiadurak () horizontalarekin osatzen angelutik abiatuz.

Beraz:

Norabide horizontalean,abiaduraren osagaia beti da konstantea eta hasierakoaren () berdina.

Norabide bertikaleko abiadura HZUA bati dagokiona da, goranzko hasierako abiaduraz. Kontuan izan behar da ezen, aukeraturiko koordenatu-sisteman, azelerazioaren osagaia negatiboa dela, eta horregatik  idatziko dugu.

Ondorioz, higikariaren abiadura bektorearen adierazpen bektoriala ondorengoa izango da:

Beste era batera:

Abiadura bektorearen modulua hauxe izango da:

POSIZIO BEKTOREA

Norabide horizontaleko higidura osatzailea, uniformea da; beraz, x koordenatuari dagokion ekuazioa HZU batena izango da:

Norabide bertikaleko osagaia den higidura, uniformeki azeleratua da; beraz, y koordenatuari dagokion ekuazioa HZUA batena da:

Posizio bektorea, bi norabideetako higidurei dagozkien posizio-bektoreen batura bektoriala da:

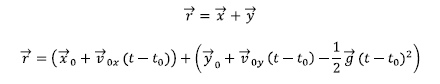
Beste era batera:

Moduluaren balioa hauxe izango da:

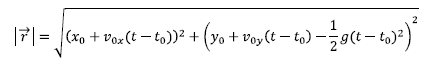
x eta y, posizioa ematen diguten ekuazioetan t denbora ezabatzen badugu, ibilbidearen ekuazioa lortuko dugu:

Eta hori da irudian agertzen den parabolaren ekuazioa; horregatik esaten zaio higidura paraboliko.

PARAMETRO KARAKTERISTIKOAK

Jarraian higidura parabolikoaren parametro karakteristikoak aurkeztuko ditugu. Parametro horiek lurretik egindako tiro parabolikoaren kasuan x₀=0,y₀=0 eta t₀=0 eginez kalkulatu ditugu. (A)

Higidura-denbora

Higikaria higitzen ari deneko denbora da. Denbora hori kalkulatzeko, gorputza lurrera heltzean, bere bertikaleko posizioa nulua dela (y=0) kontutan hartu behar dugu.

Bigarren mailako ekuazioa denez bi soluzio lortuko ditugu:

Lortutako bigarren balioan v_0y-ren balioa ordezkatuz:

Irispena edo helmena

Higikariak egiten duen distantzia horizontala da.

Irispenaren balioa lortzeko, x koordenatuaren ekuazioan higidura-denboraren balioa ordezkatuko dugu:

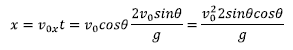
Erlazio trigonometrikoak aintzat harturik:

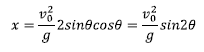
Altuera maximoa

Higikariak altuera maximoa lortzerakoan, bere goranzko abiadura bertikala deuseztatu egiten da (). Hots,  deneko denbora unean gertatuko da hori. T-ren balioa lortuz:

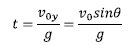
Balio hau ordezkatu egingo dugu y koordenatuaren ekuazioan:

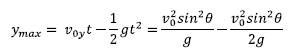
Beraz:

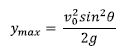
Kontutan hartzekoak

A) Goran ikus daitezkeen planteamenduak bakar-bakarrik onargarriak dira aurreko paragrafoan zehaztutako baldintzak betetzen badira. Aurrekoak betetzen ez badira, kasu bakoitzerako azterketa berezia egin beharko dugu.

B) Gorputz bat lurretik altuera jakin batera dagoen puntu jakin batetik, honekiko norabide paraleloan jaurtitzen deneko higidurari, TIRO HORIZONTALA deritzo. Horizontalean hegaz doan hegazkin batetik jausten uzten dugun gorputz baten higidura ere era horretakoa da; kasu horretan, gorputzaren hasierako abiadura hegazkinaren abiaduraren berdina da. Tori horizontala jaurtiketa angelua, θ=0º duen higidura parabolikoa da, beraz. Higidura hori eta higidura parabolikoz ari den gorputz batek altuera maximotik aurrera hartzen duen higidura berdinak dira. Beraz, higidura horren ibilbideak parabola izan behar du, irudian agertzen den moduan.

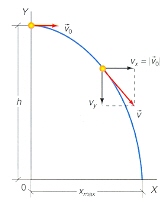
Higidura mota honen ebazpen matematikoa gauzatzeko, tiro parabolikorako lorturiko ekuazioetatik abia gaitezke. Aintzat hartu beharra daukagu, halere, tiro horizontalean v_0y=0 eta y₀=h izango direla.

Praktikatzeko

Ebaztutako ariketa

23.- Mutiko batek pilota bat botatzen du 10 m/s-ko abiaduraz eta 45º-ko angelua osatuz x ardatzarekin. Pilotak 3 m-ko distantziara dagoen pareta bat jotzen du.

1. Noiz egiten du igotzerakoan ala jeisterakoan?.
2. Zein altueran jotzen du?.
3. Zenbateko abiadurarekin?. (Ebazpena – pdf, 294 Kb)

Proposatutako ariketak

24.- 45 m-ko altuera duen dorre baten gainetik, harri bat botatzen da abiadura horizontal batekin. Dorrearen oinetik harria erori den punturaino 60 metro baldin badaude:

1. Zer abiadura horizontal eman zaio harriari?.
2. Zer denbora behar du harriak lurra jotzeko?.

25.- 30º-ko inklinazioa duen teilatu batetik gorputz bat erortzen da 15 m/s-ko abiaduraz. kalearen zabalera 20 m bada eta etxearen altuera 30 m-koa:

1. Esan ezazu gorputza lurrera eroriko den edo aurrez-aurreko etxearen kontra joko duen?.
2. Lehenengo kasuan azaldu ezazu lurreko zer distantziatara eroriko den eta bigarren kasuan zer altueran joko duen etxea.

26.- Hegaldi horizontala daraman hegazkin batetik pakete bat askatzen da. Paketearen ibilbidean airearen marruskadura kontuan hartzen ez badugu eta hegazkinak bere abiadura handitzen badu, askatzen dugun bigarren pakete batek lurrera heltzeko beharko duen denbora: (TW226)

1. Handiagoa da
2. Ez da aldatzen
3. Txikiagoa da
4. Altueraren araberakoa da

27.- Kainoi batek proiektil bat jaurtitzen du 200 m/s-ko abiaduraz horizontalarekiko 15º-ko angelua osatuz. Zera jakin nahi da:

1. Horizontalarekiko proiektilak lortuko duen irismen teorikoa
2. Lurrera heltzerakoan proeiktilaren abiaduraren modulua eta bere norabideak horizontalarekin osatuko duen angelua.
3. Lortuko lukeen irismen maximoaren erdian 300 m-ko muino bat egongo balitz, proeiktilak honekin topo egingo luke?. Zergatik?. Ondo esplikatu.
4. Erantzuna baiezkoa bada, leku beretik eta kainoi berarekin proeiktilaren objektiboa mantendu nahiko bagenu, zein irtenbide okurritzen zaizu?. Ahal den kasuan egitzazu beharrezkoak diren kalkuluak.

28.- Gauza jakina da Holandan neguak oso hotzak izaten direla. Amsterdam-eko kanaletako ura zeharo izoztuta egoten da aste askotan zehar eta bertan, jende ugari ibiltzen da patinatzen izotzaren gainean. Patinatzaile hauetako batek kanal nagusia zeharkatu nahi du beste ertzean dagoen pareko puntura zuzenduz, horretarako 10 m/s-ko abiadura hartzen duelarik. Une horretan, eta bat-batean, azelerazio konstantedun haize bolada bortitz batek bere higiduraren norabidea aldatzen du, aurkako ertzera abiapuntua baino 5 m beherago heltzen delarik. Kanala zeharkatzeko guztira 1,5 s behar izan baditu, kalkulatu:

1. Kanalaren zabalera
2. Haize boladaren azelerazioa
3. Pareko ertzera heltzerakoan patinatzaileak duen abiadura eta bere norabidea
4. Marraztu patinatzaileak deskribaturiko ibilbidea eta aurkitu bere ekuazioa